Chapter 4 Data Structures in R

This chapter delves into the following data structures and their associated R functions:

Scalar: A singular data point, such as a string or a number.
Vector: A one-dimensional array that contains elements of the same type.
Matrix (matrix): A two-dimensional array that contains elements of the same type.
List (list): A one-dimensional array capable of storing various data types.
Data Frame (data.frame): A two-dimensional array that can accommodate columns of different types.
Tibble (tbl_df): Introduced by the tibble package (Müller and Wickham 2023), a tibble is a modern take on the data frame. As a component of the tidyverse (Wickham 2023c), tibbles offer improved features for better usability.
Data Table (data.table): A high-performance extension of data frames by the data.table package (Barrett et al. 2024), crafted for efficient operations on large datasets.
Extensible Time Series (xts): A specialized data frame offered by the xts package (Ryan and Ulrich 2024b), designed explicitly for time series data.

Understanding the data structure of variables is crucial because it determines the operations and functions that can be applied to them.

4.1 Scalar

Scalars in R are variables holding single objects, such as a number, a string, a logical value, or a date.

# Numeric (a.k.a. Double)
w <- 5.5  # w is a decimal number.
class(w)  # Returns "numeric".

# Integer
x <- 10L  # The L tells R to store x as an integer instead of a decimal number.
class(x)  # Returns "integer".

# Complex
u <- 3 + 4i # u is a complex number, where 3 is real and 4 is imaginary.
class(u)  # Returns "complex".

# Character
y <- "Hello, World!"  # y is a character string.
class(y)  # Returns "character".

# Logical
z <- TRUE  # z is a logical value.
class(z)  # Returns "logical".

# Date
z <- as.Date("2022-08-12")  # z is a Date value.
class(z)  # Returns "Date".

# Time
z <- as.POSIXct("2022-08-12 22:30:12", tz = "America/Chicago")  # z is a time value.
class(z)  # Returns "POSIXct".

## [1] "numeric"
## [1] "integer"
## [1] "complex"
## [1] "character"
## [1] "logical"
## [1] "Date"
## [1] "POSIXct" "POSIXt"

Further discussions on functions pertaining to these data types can be found in Chapters 3.2 and 3.3.

4.2 Vector

In R, a vector is a homogeneous sequence of elements, meaning they must all be of the same data type. As such, a vector can hold multiple numbers, but it cannot mix types, such as having both numbers and words. The function c() (for combine) can be used to create a vector.

# Numeric vector
numeric_vector <- c(5, 2, 3, 4, 1)
class(numeric_vector)  # Returns "numeric".

# Character vector
character_vector <- c("Hello", "World", "!")
class(character_vector)  # Returns "character".

# Logical vector
logical_vector <- c(TRUE, FALSE, TRUE)
class(logical_vector)  # Returns "logical".

# Date vector
date_vector <- as.Date(c("2022-08-12", "2022-08-30", "2022-09-03"))
class(date_vector)  # Returns "Date".

# Unordered factor
unordered_factor <- factor(x = c("male", "male", "female", "male", "female"),
                           levels = c("male", "female", "other"),
                           ordered = FALSE)
class(unordered_factor)  # Returns "factor".

# Ordered factor
ordered_factor <- factor(x = c("L", "L", "H", "L", "M", "H", "M", "M", "H"),
                         levels = c("L", "M", "H"),
                         ordered = TRUE)
class(ordered_factor)  # Returns "ordered" "factor".

## [1] "numeric"
## [1] "character"
## [1] "logical"
## [1] "Date"
## [1] "factor"
## [1] "ordered" "factor"

In R, the class() function labels both scalars and vectors by their data type, not by their dimension. Consequently, a single integer and a vector of integers are both labeled as “integer”. This perspective aligns with the idea that a scalar is essentially a vector with only one element.

For an overview of vector operations, see Chapters 3.2.7 and 3.2.8.

4.3 Matrix (`matrix`)

A matrix in R is a two-dimensional array comprising both rows and columns. Every element within the matrix must belong to the same data type, be it numeric, character, or otherwise.

4.3.1 Create a Matrix

Matrices can be formed using the matrix() function, and its important inputs include:

data: The elements that constitute the matrix.
nrow and ncol: Specify the number of rows and columns, respectively.
byrow: A logical value. If set to TRUE, the matrix is filled by rows. If FALSE (the default), it’s filled by columns.

# Create a 3x3 numeric matrix, column-wise (default behavior)
numeric_matrix <- matrix(data = 1:9, ncol = 3)
print(numeric_matrix)

##      [,1] [,2] [,3]
## [1,]    1    4    7
## [2,]    2    5    8
## [3,]    3    6    9

# Create a 2x3 character matrix, row-wise
character_matrix <- matrix(data = letters[1:6], ncol = 3, byrow = TRUE)
print(character_matrix)

##      [,1] [,2] [,3]
## [1,] "a"  "b"  "c" 
## [2,] "d"  "e"  "f"

4.3.2 Inspect a Matrix

To gain an understanding of the type and structure of a matrix, utilize the following functions:

# Investigate numeric matrix
class(numeric_matrix)        # Outputs "matrix".
is.matrix(numeric_matrix)    # Outputs TRUE.
typeof(numeric_matrix)       # Outputs "integer".

## [1] "matrix" "array" 
## [1] TRUE
## [1] "integer"

# Investigate character matrix
class(character_matrix)      # Outputs "matrix".
is.matrix(character_matrix)  # Outputs TRUE.
typeof(character_matrix)     # Outputs "character".

## [1] "matrix" "array" 
## [1] TRUE
## [1] "character"

To ascertain the dimensions of a matrix, one can employ the nrow(), ncol(), and dim() functions:

# Retrieve row count
(rows_count <- nrow(character_matrix))

## [1] 2

# Retrieve column count
(columns_count <- ncol(character_matrix))

## [1] 3

# Obtain overall dimensions
dim(character_matrix) # Returns a vector: c(rows_count, columns_count)

## [1] 2 3

The head() and tail() functions retrieve the initial and final n rows of a matrix, respectively, with a default value of n = 6. These functions are handy when the matrix has a substantial number of rows, making it difficult to display the entire matrix in the R console.

# Extract the first two rows
head(numeric_matrix, n = 2)

##      [,1] [,2] [,3]
## [1,]    1    4    7
## [2,]    2    5    8

# Extract the last row
tail(character_matrix, n = 1)

##      [,1] [,2] [,3]
## [2,] "d"  "e"  "f"

If a matrix has a large number of columns, making it challenging to display even with head() or tail(), RStudio offers the View() function, which presents the matrix in a spreadsheet format. Note that View() is specific to RStudio and isn’t part of base R.

# Display the matrix in a spreadsheet-like viewer
View(character_matrix)

Moreover, the summary() function delivers a collection of statistical measures for every column in a numeric matrix. This function is invaluable as it offers insights that might not be immediately evident from looking at the data.

# Generate statistical summaries for the columns of a numeric matrix
summary(numeric_matrix)

##        V1            V2            V3     
##  Min.   :1.0   Min.   :4.0   Min.   :7.0  
##  1st Qu.:1.5   1st Qu.:4.5   1st Qu.:7.5  
##  Median :2.0   Median :5.0   Median :8.0  
##  Mean   :2.0   Mean   :5.0   Mean   :8.0  
##  3rd Qu.:2.5   3rd Qu.:5.5   3rd Qu.:8.5  
##  Max.   :3.0   Max.   :6.0   Max.   :9.0

4.3.3 Select and Modify

You can select and modify specific elements, rows, or columns using indexing:

# Access the element in the 2nd row and 1st column
character_matrix[2, 1]

## [1] "d"

# Access the entire second row
character_matrix[2, ]

## [1] "d" "e" "f"

# Access the second row but retain the matrix structure
character_matrix[2, , drop = FALSE]

##      [,1] [,2] [,3]
## [1,] "d"  "e"  "f"

# Assign a specific value to an element
numeric_matrix[2, 1] <- 99
print(numeric_matrix)

##      [,1] [,2] [,3]
## [1,]    1    4    7
## [2,]   99    5    8
## [3,]    3    6    9

4.3.4 Add Labels

For better clarity, rows and columns can be named:

# Constructing a matrix with labeled rows and columns
labeled_matrix <- matrix(data = 1:4, ncol = 2, 
                         dimnames = list(c("Row1", "Row2"), 
                                         c("Col1", "Col2")))
print(labeled_matrix)

##      Col1 Col2
## Row1    1    3
## Row2    2    4

# Retrieving and modifying labels
colnames(labeled_matrix)

## [1] "Col1" "Col2"

rownames(labeled_matrix) <- c("First_Row", "Second_Row")
print(labeled_matrix)

##            Col1 Col2
## First_Row     1    3
## Second_Row    2    4

4.3.5 Handle Missing Values

Matrices in R can also contain missing values, represented by NA:

# Matrix with NA values
mat_with_na <- matrix(data = c(1, 2, NA, 4, 5, 6, 7, 8, 9), nrow = 3)
print(mat_with_na)

##      [,1] [,2] [,3]
## [1,]    1    4    7
## [2,]    2    5    8
## [3,]   NA    6    9

# Identify NA values
is.na(mat_with_na)

##       [,1]  [,2]  [,3]
## [1,] FALSE FALSE FALSE
## [2,] FALSE FALSE FALSE
## [3,]  TRUE FALSE FALSE

# Replace NA with a specified value
mat_replaced_na <- mat_with_na
mat_replaced_na[is.na(mat_replaced_na)] <- 0

# Remove entire rows with NA values
cleaned_mat <- na.omit(mat_with_na)
print(cleaned_mat)

##      [,1] [,2] [,3]
## [1,]    1    4    7
## [2,]    2    5    8
## attr(,"na.action")
## [1] 3
## attr(,"class")
## [1] "omit"

4.3.6 Element-Wise Operations

In R, matrices support a variety of operations that act on their elements. When you use typical arithmetic operators like *, +, -, and / with matrices, they operate element-wise. This means that the operation is applied to each corresponding pair of elements from the two matrices.

# Define matrix A
(A <- matrix(1:4, nrow = 2))

##      [,1] [,2]
## [1,]    1    3
## [2,]    2    4

# Define matrix B of equal size than A
(B <- matrix(5:8, nrow = 2))

##      [,1] [,2]
## [1,]    5    7
## [2,]    6    8

# Element-wise multiplication
A * B

##      [,1] [,2]
## [1,]    5   21
## [2,]   12   32

# Element-wise addition
A + B

##      [,1] [,2]
## [1,]    6   10
## [2,]    8   12

Note: For element-wise operations, the matrices should have the same dimensions. If they differ, R will attempt to recycle values, which can result in unexpected behavior.

4.3.7 Linear Algebra Operations

Beyond element-wise operations, R provides a variety of functions and operators to perform linear algebra operations on matrices.

Transpose t():
The transpose of a matrix $A$, denoted as $A^{\prime}$, is obtained by flipping it over its diagonal. This interchanges its rows and columns.

(A <- matrix(1:6, nrow = 2))  # Matrix A

##      [,1] [,2] [,3]
## [1,]    1    3    5
## [2,]    2    4    6

t(A)                          # Transpose of matrix A

##      [,1] [,2]
## [1,]    1    2
## [2,]    3    4
## [3,]    5    6

Matrix Multiplication %*%: Matrix multiplication, unlike element-wise multiplication *, uses the %*% operator. It performs the standard matrix multiplication operation, where each element of the resulting matrix is the sum of the products of elements from the corresponding rows of the first matrix (A) and the corresponding columns of the second matrix (B).

For example, if $A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}$ and $B = \begin{bmatrix} w & x \\ y & z \end{bmatrix}$, then the result of element-wise multiplication A * B will be: $A \odot B = \begin{bmatrix} a \cdot w & b \cdot x \\ c \cdot y & d \cdot z \end{bmatrix}$, whereas the result of matrix multiplication A %*% B will be: $A B = \begin{bmatrix} (a \cdot w + b \cdot y) & (a \cdot x + b \cdot z) \\ (c \cdot w + d \cdot y) & (c \cdot x + d \cdot z) \end{bmatrix}$.
```
(A <- matrix(1:4, nrow = 2))  # Matrix A
(B <- matrix(5:8, nrow = 2))  # Matrix B
A * B                         # Element-wise multiplication
A %*% B                       # Matrix multiplication AB
```
```
##      [,1] [,2]
## [1,]    1    3
## [2,]    2    4
##      [,1] [,2]
## [1,]    5    7
## [2,]    6    8
##      [,1] [,2]
## [1,]    5   21
## [2,]   12   32
##      [,1] [,2]
## [1,]   23   31
## [2,]   34   46
```
Crossproduct crossprod(A, B): Computes the matrix product $A'B$, where $A'$ is the transpose of matrix $A$. It’s essentially a faster version of computing the transpose of $A$ followed by the regular matrix multiplication with $B$.
```
crossprod(A, B)  # Equivalent to t(A) %*% B
```
```
##      [,1] [,2]
## [1,]   17   23
## [2,]   39   53
```
Kronecker Product kronecker(A, B): The Kronecker product, often denoted by $\otimes$, is an operation that takes two matrices and produces a block matrix. In R, it’s computed using the function kronecker().

For two matrices $A$ and $B$, the Kronecker product $A \otimes B$ will have the matrix $A$ scaled by each element of matrix $B$.

For example, if $A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}$ and $B = \begin{bmatrix} w & x \\ y & z \end{bmatrix}$, then $A \otimes B = \begin{bmatrix} a \cdot w & a \cdot x & b \cdot w & b \cdot x \\ a \cdot y & a \cdot z & b \cdot y & b \cdot z \\ c \cdot w & c \cdot x & d \cdot w & d \cdot x \\ c \cdot y & c \cdot z & d \cdot y & d \cdot z \end{bmatrix}$.
```
kronecker(A, B)
```
```
##      [,1] [,2] [,3] [,4]
## [1,]    5    7   15   21
## [2,]    6    8   18   24
## [3,]   10   14   20   28
## [4,]   12   16   24   32
```
Vec Operator: The vec operator is used to stack the columns of a matrix on top of each other, creating a single column vector. In R, you can achieve this by using the c() function or the as.vector() function to concatenate the columns of a matrix into a single vector, and then using the matrix() function to specify that the resulting vector is a column vector.

For example, if $A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}$, then $\text{vec}(A) = \begin{bmatrix} a \\ c \\ b \\ d \end{bmatrix}$.
```
# Use the vec operator to stack the columns of matrix A
matrix(c(A), ncol = 1)
```
```
##      [,1]
## [1,]    1
## [2,]    2
## [3,]    3
## [4,]    4
```
In this example, vec(A) stacks the columns of matrix_A on top of each other to create a single column vector.
Matrix Inversion solve():
The inverse of a matrix $A$ (if it exists), denoted as $A^{-1}$, is a matrix $B$ such that the product of $A$ and $B$ (in that order) is the identity matrix: $AB=I$. Use solve() to compute the inverse.
```
solve(A)  # Inverse of matrix A
```
```
##      [,1] [,2]
## [1,]   -2  1.5
## [2,]    1 -0.5
```
Solving Linear Systems with solve(A, B):
If you have a matrix equation of the form $A X = B$, you can solve for matrix $X$ using solve(A, B). This approach is more efficient than computing solve(B) %*% A.
```
solve(A, B) # Determines X in the equation AX = B
```
```
##      [,1] [,2]
## [1,]   -1   -2
## [2,]    2    3
```

Matrix Exponentiation:
Raising a matrix to a power ($n$) is not as straightforward as using the ^ operator. The %^% operator from the expm package (Maechler, Dutang, and Goulet 2024) facilitates matrix exponentiation in accordance with linear algebra rules.

library(expm)
A ^ 2    # Element-wise squaring of A

##      [,1] [,2]
## [1,]    1    9
## [2,]    4   16

A %^% 2  # Matrix squaring of A, equivalent to A %*% A

##      [,1] [,2]
## [1,]    7   15
## [2,]   10   22

A %^% 3  # Computes A %*% A %*% A

##      [,1] [,2]
## [1,]   37   81
## [2,]   54  118

Eigenvalues and Eigenvectors eigen():
The eigen() function is used to compute the eigenvalues and eigenvectors of a matrix.

eigen(A)

## eigen() decomposition
## $values
## [1]  5.3722813 -0.3722813
## 
## $vectors
##            [,1]       [,2]
## [1,] -0.5657675 -0.9093767
## [2,] -0.8245648  0.4159736

Determinant det():
You can compute the determinant of a matrix using the det() function.
```
det(A)  # Determinant of matrix A
```
```
## [1] -2
```
Matrix Rank qr():
The rank of a matrix, which is the dimension of the column space, can be determined using the qr() function.
```
qr(A)$rank  # Rank of matrix A
```
```
## [1] 2
```

Singular Value Decomposition svd(): Computes the singular value decomposition of a matrix.

svd_result <- svd(A)
svd_result$u  # Left singular vectors

##            [,1]       [,2]
## [1,] -0.5760484 -0.8174156
## [2,] -0.8174156  0.5760484

svd_result$d  # Singular values

## [1] 5.4649857 0.3659662

svd_result$v  # Right singular vectors

##            [,1]       [,2]
## [1,] -0.4045536  0.9145143
## [2,] -0.9145143 -0.4045536

Cholesky Decomposition chol(): Performs the Cholesky decomposition on a positive-definite square matrix.

# Define positive definite symmetric matrix C
(C <- matrix(c(4, 2, 2, 3), nrow = 2))

##      [,1] [,2]
## [1,]    4    2
## [2,]    2    3

# Compute Cholesky decomposition
chol(C)

##      [,1]     [,2]
## [1,]    2 1.000000
## [2,]    0 1.414214

LU Decomposition Matrix::lu(): The lu() function from the Matrix package (Bates, Maechler, and Jagan 2024) decomposes a matrix into a product of a lower triangular and an upper triangular matrix.

library("Matrix")
lu(A)

## LU factorization of Formal class 'denseLU' [package "Matrix"] with 4 slots
##   ..@ x       : num [1:4] 2 0.5 4 1
##   ..@ perm    : int [1:2] 2 2
##   ..@ Dim     : int [1:2] 2 2
##   ..@ Dimnames:List of 2
##   .. ..$ : NULL
##   .. ..$ : NULL

QR Decomposition qr(): Decomposes a matrix into a product of an orthogonal and a triangular matrix.

qr(A)

## $qr
##            [,1]       [,2]
## [1,] -2.2360680 -4.9193496
## [2,]  0.8944272 -0.8944272
## 
## $rank
## [1] 2
## 
## $qraux
## [1] 1.4472136 0.8944272
## 
## $pivot
## [1] 1 2
## 
## attr(,"class")
## [1] "qr"

Condition Number kappa(): Estimates the condition number of a matrix, which provides insight into the stability of matrix computations.
```
kappa(A)
```
```
## [1] 18.77778
```
Matrix Norm Matrix::norm(): The norm() function from the Matrix package (Bates, Maechler, and Jagan 2024) computes various matrix norms.
```
library("Matrix")
norm(A, type = "F")  # Frobenius norm
```
```
## [1] 5.477226
```

Remember to always ensure that the matrices you’re using with these functions meet the necessary preconditions (e.g., being square, positive-definite, etc.) required for each operation.

4.3.8 Combine Matrices

Matrices in R can be joined together using various functions. The most straightforward methods are rbind() for row-wise binding and cbind() for column-wise binding:

# Create matrices with identical column and row numbers
x <- matrix(data = 1:4, ncol = 2)
y <- matrix(data = 101:104, ncol = 2)

# Row-wise combination of matrices with same column number
rbind(x, y)

##      [,1] [,2]
## [1,]    1    3
## [2,]    2    4
## [3,]  101  103
## [4,]  102  104

# Column-wise combination of matrices with same row number
cbind(x, y)

##      [,1] [,2] [,3] [,4]
## [1,]    1    3  101  103
## [2,]    2    4  102  104

Additionally, when combining multiple matrices, the Reduce() function can be quite handy:

# Create additional matrix with identical column number
z <- matrix(data = 201:206, ncol = 2)

# Use Reduce with rbind to combine multiple matrices row-wise
Reduce(f = rbind, x = list(x, y, z))

##      [,1] [,2]
## [1,]    1    3
## [2,]    2    4
## [3,]  101  103
## [4,]  102  104
## [5,]  201  204
## [6,]  202  205
## [7,]  203  206

The Reduce() function, detailed in Chapter 3.5.10, is a prominent example of advanced higher-order functions. It facilitates consecutive operations over a list or vector. In the given context, it employs the rbind() function repeatedly to merge matrices. This technique becomes particularly beneficial when dealing with a variable or large number of matrices.

For example, to compute powers of matrices, you can use the Reduce() function to create a custom operation instead of relying on the %^% function from the expm package discussed in Chapter 4.3.7:

# Define a custom function for matrix exponentiation
`%**%` <- function(MAT, n) 
    Reduce(f = `%*%`, x = replicate(n = n, expr = MAT, simplify = FALSE))

# Demonstrate the sixth power of matrix x (contrast with element-wise exponentiation)
x%**%6
x^6

##      [,1]  [,2]
## [1,] 5743 12555
## [2,] 8370 18298
##      [,1] [,2]
## [1,]    1  729
## [2,]   64 4096

In this revised version, the custom function %**% employs the Reduce() function to successively multiply the matrix with itself, achieving matrix exponentiation.

4.3.9 Apply Family

Apply functions are instrumental in conducting operations on matrices efficiently, offering an optimized alternative to loops (see Chapter 3.5.9). While the sapply function discussed in Chapter 3.5.9 applies a function to each element of a vector, the apply function is specialized for matrices and applies a function to each row or column of that matrix.

# Define a numeric matrix
(A <- matrix(1:9, ncol = 3))

##      [,1] [,2] [,3]
## [1,]    1    4    7
## [2,]    2    5    8
## [3,]    3    6    9

# Calculating the maximum of each row
apply(X = A, MARGIN = 1, FUN = function(r) max(r))

## [1] 7 8 9

# Calculating the sum of each column (using compact FUN notation)
apply(X = A, MARGIN = 2, FUN = max)

## [1] 3 6 9

The inputs for the apply function include:

X: Specifies the matrix or array.
MARGIN: Designates 1 for operations across rows and 2 for columns.
FUN: The function to be executed (examples include sum, mean).

For those seeking expedited calculations for specific functions like sum() or mean(), R offers faster alternatives such as rowSums(), colSums(), colMeans(), and rowMeans().

# Summation across rows
apply(X = A, MARGIN = 1, FUN = sum)
rowSums(A) # A faster alternative

## [1] 12 15 18
## [1] 12 15 18

# Averaging across columns
apply(X = A, MARGIN = 2, FUN = mean)
colMeans(A) # A faster alternative

## [1] 2 5 8
## [1] 2 5 8

The sweep() function allows for efficient array manipulations, such as subtraction or division, across rows or columns using summary statistics. Specifically, it combines the capabilities of apply() and rep() to operate element-wise on a matrix. This is particularly useful when performing operations that require using a summary statistic—such as a mean—across all elements of a matrix. For example, one could use sweep() to demean a matrix by subtracting the mean of each column from every element in that respective column.

# Define a numeric matrix
(B <- matrix(c(1, 4, 6, 8, 109, 107, 104, 105), ncol = 2))

##      [,1] [,2]
## [1,]    1  109
## [2,]    4  107
## [3,]    6  104
## [4,]    8  105

# Calculate mean of each column
(col_means <- colMeans(B))

## [1]   4.75 106.25

# Use sweep to subtract each column's mean from each element in that column
sweep(x = B, MARGIN = 2, STATS = col_means, FUN = "-")

##       [,1]  [,2]
## [1,] -3.75  2.75
## [2,] -0.75  0.75
## [3,]  1.25 -2.25
## [4,]  3.25 -1.25

Manually achieving the same effect would involve a combination of apply(), rep(), and element-wise operations:

# Replicate the means to match the dimensions of the original matrix
(rep_means <- matrix(rep(col_means, each = nrow(B)), nrow = nrow(B)))

##      [,1]   [,2]
## [1,] 4.75 106.25
## [2,] 4.75 106.25
## [3,] 4.75 106.25
## [4,] 4.75 106.25

# Subtract the replicated means from the original matrix element-wise
B - rep_means

##       [,1]  [,2]
## [1,] -3.75  2.75
## [2,] -0.75  0.75
## [3,]  1.25 -2.25
## [4,]  3.25 -1.25

In conclusion, matrices form an integral component of R, especially for multivariate analysis and linear algebra tasks. A comprehensive understanding of matrix operations in R can substantially elevate your data manipulation and analysis capabilities.

4.4 List (`list`)

A list (list) in R serve as an ordered collection of objects. In contrast to vectors, elements within a list are not required to be of the same type. Moreover, some list elements may store multiple sub-elements, allowing for complex nested structures. For instance, a single element of a list might itself be a matrix or another list.

4.4.1 Create a List

Lists can be formed using the list() function:

# Constructing a list
list_sample <- list(name = "John", 
                    age = 25, 
                    is_student = TRUE,
                    scores = c(88, 90, 78, 92), 
                    grade = "B",
                    relationships = list(friends = c("Marc", "Victor", "Peter"), 
                                         parents = c("Valerie", "Bob"),
                                         partner = NA))
print(list_sample)

## $name
## [1] "John"
## 
## $age
## [1] 25
## 
## $is_student
## [1] TRUE
## 
## $scores
## [1] 88 90 78 92
## 
## $grade
## [1] "B"
## 
## $relationships
## $relationships$friends
## [1] "Marc"   "Victor" "Peter" 
## 
## $relationships$parents
## [1] "Valerie" "Bob"    
## 
## $relationships$partner
## [1] NA

The elements within the list (list_sample) encompass diverse data types: character strings (name and grade), numeric values (age), logical indicators (is_student), vectors (scores), and nested lists (relationships). This shows the versatility of lists in R, capable of storing various data types and structures.

You can also convert other objects (e.g., vectors) into lists using the as.list() function:

# Transform a numeric vector into a list
converted_list <- as.list(1:3)

# Revert the list back to a vector
unlist(converted_list)

## [1] 1 2 3

4.4.2 Inspect a List

To identify the type and components of a list, the following functions can be utilized:

# Identify the data structure of the list
class(list_sample)    # Outputs "list".
is.list(list_sample)  # Outputs TRUE.

# Identify the data type of each element within the list
sapply(list_sample, class)

## [1] "list"
## [1] TRUE
##          name           age    is_student        scores         grade 
##   "character"     "numeric"     "logical"     "numeric"   "character" 
## relationships 
##        "list"

To determine the total count of items in a list, employ the length() function:

# Ascertain the count of items in the list
length(list_sample)

## [1] 6

To gain a comprehensive view of the list’s content and structure, the str() and summary() functions are valuable:

# Delve into the list's structure
str(list_sample)

## List of 6
##  $ name         : chr "John"
##  $ age          : num 25
##  $ is_student   : logi TRUE
##  $ scores       : num [1:4] 88 90 78 92
##  $ grade        : chr "B"
##  $ relationships:List of 3
##   ..$ friends: chr [1:3] "Marc" "Victor" "Peter"
##   ..$ parents: chr [1:2] "Valerie" "Bob"
##   ..$ partner: logi NA

# Summarize list elements
summary(list_sample)

##               Length Class  Mode     
## name          1      -none- character
## age           1      -none- numeric  
## is_student    1      -none- logical  
## scores        4      -none- numeric  
## grade         1      -none- character
## relationships 3      -none- list

4.4.3 Select and Modify

You can select and modify specific elements using indexing:

# Retrieving elements by index using double square brackets
list_sample[[2]]

## [1] 25

# Fetching elements by name with the dollar sign
list_sample$age

## [1] 25

# Another method for name-based access using double square brackets
list_sample[["age"]]

## [1] 25

# Accessing multiple elements using an index via single square bracket
list_sample[c(1, 3)]

## $name
## [1] "John"
## 
## $is_student
## [1] TRUE

# Nested lists: retrieving 'Marc' from the 'friends' sublist
list_sample$relationships$friends[1]

## [1] "Marc"

# Introducing a new element
list_sample$address <- "123 Main St"

# Adjusting an existing element
list_sample$name <- "John Travolta"

# Deleting an element
list_sample$relationships <- NULL

4.4.4 Add Labels

You can examine and modify the names of the list elements:

# Checking the names of the elements
names(list_sample)

## [1] "name"       "age"        "is_student" "scores"     "grade"     
## [6] "address"

# Modifying the element names
names(list_sample) <- c("Full Name", "Age", "Is Student", 
                        "Scores", "Grade", "Address")

4.4.5 Combine Lists

You can merge lists with the c() function:

# Create two sample lists
list_1 <- list(name = "Alice", age = 30, is_female = TRUE)
list_2 <- list(job = "Engineer", city = "New York")

# Merge the lists
merged_list <- c(list_1, list_2)
print(merged_list)

## $name
## [1] "Alice"
## 
## $age
## [1] 30
## 
## $is_female
## [1] TRUE
## 
## $job
## [1] "Engineer"
## 
## $city
## [1] "New York"

For more control over the merging position, use the append() function. It offers an after argument to specify where the second list should be inserted:

# Merge the lists, placing the second list after the second element
merged_at_position <- append(list_1, list_2, after = 2)
print(merged_at_position)

## $name
## [1] "Alice"
## 
## $age
## [1] 30
## 
## $job
## [1] "Engineer"
## 
## $city
## [1] "New York"
## 
## $is_female
## [1] TRUE

Here, the append() function inserts the elements of list_2 immediately after the second element of list_1.

To reverse the order of a list’s elements, apply the rev() function:

# Reverse the order of list elements
reversed_list <- rev(list_sample)
print(reversed_list)

## $Address
## [1] "123 Main St"
## 
## $Grade
## [1] "B"
## 
## $Scores
## [1] 88 90 78 92
## 
## $`Is Student`
## [1] TRUE
## 
## $Age
## [1] 25
## 
## $`Full Name`
## [1] "John Travolta"

4.4.6 Apply Family

The apply functions are not limited to vectors and matrices; they can be applied to lists, offering a more concise and optimized alternative to loops. This section delves into the use of apply functions with lists.

lapply: The lapply() (list-apply) function is tailored specifically for lists. It applies a given function to each element of a list and consistently returns results in list format.

# Define a sample list of numeric vectors
sample_list <- list(
    a = c(2, 4, 6),
    b = c(3, 6, 9, 12),
    c = c(4, 8)
)

# Use lapply to calculate the mean of each list element
lapply(X = sample_list, FUN = mean)

## $a
## [1] 4
## 
## $b
## [1] 7.5
## 
## $c
## [1] 6

sapply: The sapply() function (simplify-apply) aims to simplify the output, defaulting to vectors whenever feasible. Thus, unlike the lapply() function, its return type is not always a list.
```
# Compute the mean of each list element and return a vector if possible
sapply(X = sample_list, FUN = mean)
```
```
##   a   b   c 
## 4.0 7.5 6.0
```

vapply: The vapply() function (value-apply) mirrors sapply() but with an additional provision: you can designate the expected return type. This feature not only ensures consistent output format but can also boost speed in specific cases.

# Compute the mean (numeric) of each list element
vapply(X = sample_list, FUN = mean, FUN.VALUE = numeric(1))

##   a   b   c 
## 4.0 7.5 6.0

# Compute the mean (numeric) and type (character) of each list element
vapply(X = sample_list, 
       FUN = function(vec) list(mean_value = mean(vec), type = class(vec)), 
       FUN.VALUE = list(mean_value = numeric(1), type = character(1)))

##            a         b         c        
## mean_value 4         7.5       6        
## type       "numeric" "numeric" "numeric"

In summary, lists are inherently flexible and, due to this characteristic, play a pivotal role in many R tasks, from data manipulation to functional programming.

4.5 Data Frame (`data.frame`)

A data frame (data.frame) in R resembles a matrix in its two-dimensional, rectangular structure. However, unlike a matrix, a data frame allows each column to contain a different data type. Therefore, within each column (or vector), the elements must be homogeneous, but different columns can accommodate distinct types. Typically, when importing data into R, the default object type used is a data frame.

4.5.1 Create a Data Frame

Data frames can be formed using the data.frame() function:

# Create vectors for the data frame
names <- c("Anna", "Ella", "Sophia")
ages <- c(23, NA, 26)
female <- c(TRUE, TRUE, TRUE)
grades <- factor(c("A", "B", "A"), levels = rev(LETTERS[1:6]), ordered = TRUE)
major <- c("Math", "Biology", "Physics")

# Construct the data frame
students_df <- data.frame(name = names, 
                          age = ages, 
                          female = female,
                          grade = grades, 
                          major = major)
print(students_df)

##     name age female grade   major
## 1   Anna  23   TRUE     A    Math
## 2   Ella  NA   TRUE     B Biology
## 3 Sophia  26   TRUE     A Physics

In the above code chunk, we observe that like a matrix, every column in a data frame possesses an identical length (3 rows). However, the first and fifth columns are composed of character data (name, major), while the second column comprises numeric data (age), the third column consists of logical values (female), and the fourth column is an ordered factor (grade). This capacity to host varied data types in separate columns is what sets data frames apart from matrices.

4.5.2 Inspect a Data Frame

To identify the type and components of a data frame, the following functions can be utilized:

# Identify the data structure of the data frame
class(students_df)          # Outputs "data.frame".
is.data.frame(students_df)  # Outputs TRUE

## [1] "data.frame"
## [1] TRUE

# Identify the data type of each column within the data frame
sapply(students_df, class)

## $name
## [1] "character"
## 
## $age
## [1] "numeric"
## 
## $female
## [1] "logical"
## 
## $grade
## [1] "ordered" "factor" 
## 
## $major
## [1] "character"

Many matrix operations are compatible with data frames. For instance, to determine the dimensions of a data frame, the functions nrow(), ncol(), and dim() can be used, analogous to their applications with matrices discussed in Chapter 4.3:

# Retrieve row count
(rows_count <- nrow(students_df))

## [1] 3

# Retrieve column count
(columns_count <- ncol(students_df))

## [1] 5

# Obtain overall dimensions
dim(students_df) # Returns a vector: c(rows_count, columns_count)

## [1] 3 5

The head() and tail() functions are employed to extract the first and last n rows of a data frame, respectively, where n is defaulted to 6. They are particularly beneficial when working with large data frames, as displaying the entirety in the R console becomes unwieldy.

# Retrieve the first two rows
head(students_df, n = 2)

##   name age female grade   major
## 1 Anna  23   TRUE     A    Math
## 2 Ella  NA   TRUE     B Biology

# Obtain the second-last row
head(tail(students_df, n = 2), n = 1)

##   name age female grade   major
## 2 Ella  NA   TRUE     B Biology

For data frames with many columns, which can be cumbersome to display fully using head() or tail(), RStudio’s View() function is beneficial. It displays the data frame in a spreadsheet style. It’s worth noting that the View() function is exclusive to RStudio and is not a feature of base R.

# Open the data frame in RStudio's spreadsheet-style viewer
View(students_df)

Furthermore, the summary() and str() functions provide detailed insights into a data frame’s columns in terms of their composition and characteristics. These tools are essential for understanding facets of the data that might not be immediately apparent from a cursory glance.

# Inspect the data frame's structure
str(students_df)

## 'data.frame':    3 obs. of  5 variables:
##  $ name  : chr  "Anna" "Ella" "Sophia"
##  $ age   : num  23 NA 26
##  $ female: logi  TRUE TRUE TRUE
##  $ grade : Ord.factor w/ 6 levels "F"<"E"<"D"<"C"<..: 6 5 6
##  $ major : chr  "Math" "Biology" "Physics"

# Gather a comprehensive overview of the data frame
summary(students_df)

##      name                age         female        grade    major          
##  Length:3           Min.   :23.00   Mode:logical   F:0   Length:3          
##  Class :character   1st Qu.:23.75   TRUE:3         E:0   Class :character  
##  Mode  :character   Median :24.50                  D:0   Mode  :character  
##                     Mean   :24.50                  C:0                     
##                     3rd Qu.:25.25                  B:1                     
##                     Max.   :26.00                  A:2                     
##                     NA's   :1

4.5.3 Select and Modify

Elements within a data frame can be accessed, modified, or created using various indexing methods:

# Retrieve specific cell: row 2, column 4
students_df[2, 4]

## [1] B
## Levels: F < E < D < C < B < A

# Obtain an entire column by its name
students_df$major

# Another method for name-based column access
students_df[["major"]]

# Yet another method for name-based column access
students_df[, "major"]

## [1] "Math"    "Biology" "Physics"
## [1] "Math"    "Biology" "Physics"
## [1] "Math"    "Biology" "Physics"

# Obtain an entire column while retaining the data frame structure
students_df["major"]

##     major
## 1    Math
## 2 Biology
## 3 Physics

# Access multiple columns by their names
students_df[, c("name", "grade")]

# Another method for name-based multiple column access
students_df[c("name", "grade")]

##     name grade
## 1   Anna     A
## 2   Ella     B
## 3 Sophia     A
##     name grade
## 1   Anna     A
## 2   Ella     B
## 3 Sophia     A

# Extract rows based on specific criteria
selected_rows = students_df$age > 24 & students_df$grade == "A"
students_df[selected_rows, ]

##     name age female grade   major
## 3 Sophia  26   TRUE     A Physics

# Introduce a new column (ensuring the vector's length matches the number of rows)
students_df$gpa <- c(3.7, 3.4, 3.9)
print(students_df)

##     name age female grade   major gpa
## 1   Anna  23   TRUE     A    Math 3.7
## 2   Ella  NA   TRUE     B Biology 3.4
## 3 Sophia  26   TRUE     A Physics 3.9

# Delete a column
students_df$female <- NULL
print(students_df)

##     name age grade   major gpa
## 1   Anna  23     A    Math 3.7
## 2   Ella  NA     B Biology 3.4
## 3 Sophia  26     A Physics 3.9

The `with()` Function

The with() function is an indirect function that simplifies operations on data frame columns by eliminating the need for constant data frame referencing.

For instance, when working with a data frame like students_df, the conventional way to concatenate columns name and major would require referencing the data frame explicitly using students_df$name and students_df$major:

# Traditional approach: operation with repeated data frame reference
paste0(students_df$name, " studies ", students_df$major, ".")

## [1] "Anna studies Math."      "Ella studies Biology."  
## [3] "Sophia studies Physics."

Using with(), you can perform the same operation without the repeated references:

# Using with(): operation without repeated data frame reference
with(students_df, paste0(name, " studies ", major, "."))

## [1] "Anna studies Math."      "Ella studies Biology."  
## [3] "Sophia studies Physics."

Here are some more illustrative examples:

# Traditional approach: operations with repeated data frame reference
sum(students_df$gpa >= 3.5) / length(students_df$gpa) * 100     # Cum Laude Share
students_df[students_df$age > 24 & students_df$grade == "A", ]  # Select rows

# Using with(): operations without repeated data frame reference
with(students_df, sum(gpa >= 3.5) / length(gpa) * 100)          # Cum Laude Share
students_df[with(students_df, age > 24 & grade == "A"), ]       # Select rows

## [1] 66.66667
##     name age grade   major gpa
## 3 Sophia  26     A Physics 3.9
## [1] 66.66667
##     name age grade   major gpa
## 3 Sophia  26     A Physics 3.9

In summary, the with() function streamlines operations involving data frames by setting a temporary environment for computations. This can make the code more concise and reduce the likelihood of errors due to repeated data object references.

4.5.4 Add Labels

You can examine and modify the names of the data frame rows and columns:

# Names of columns and rows
colnames(students_df)

## [1] "name"  "age"   "grade" "major" "gpa"

rownames(students_df)

## [1] "1" "2" "3"

# Change column names
colnames(students_df) <- c("Name", "Age", "Grade", "Major", "GPA")

# Change the name of a specific column
colnames(students_df)[colnames(students_df) == "Major"] <- "Field of Study"
students_df

##     Name Age Grade Field of Study GPA
## 1   Anna  23     A           Math 3.7
## 2   Ella  NA     B        Biology 3.4
## 3 Sophia  26     A        Physics 3.9

4.5.5 Handle Missing Values

Data frames in R can also contain missing values, represented by NA:

# Number of missing values in each column
colSums(is.na(students_df))

##           Name            Age          Grade Field of Study            GPA 
##              0              1              0              0              0

# Remove all rows that contain missing values
na.omit(students_df)

##     Name Age Grade Field of Study GPA
## 1   Anna  23     A           Math 3.7
## 3 Sophia  26     A        Physics 3.9

# Replace missing values in 'Age' column with the mean age
students_df$Age[is.na(students_df$Age)] <- mean(students_df$Age, na.rm = TRUE)
print(students_df)

##     Name  Age Grade Field of Study GPA
## 1   Anna 23.0     A           Math 3.7
## 2   Ella 24.5     B        Biology 3.4
## 3 Sophia 26.0     A        Physics 3.9

4.5.6 Combine Data Frames

When handling data in R, there are instances where combining data from different sources or merging tables is necessary. In this context, functions like merge(), rbind(), and cbind() are invaluable. Let’s explore these functions with examples:

rbind(): This function allows you to concatenate data frames vertically, stacking one on top of the other. It is essential that the columns of both data frames match in both name and order:

# Create data frames with identical column names
(students_2022 <- data.frame(Name = c("Alice", "Bob"), Age = c(21, 22)))
(students_2023 <- data.frame(Name = c("Charlie", "David"), Age = c(23, 24)))

##    Name Age
## 1 Alice  21
## 2   Bob  22
##      Name Age
## 1 Charlie  23
## 2   David  24

# Combine data frames by rows
rbind(students_2022, students_2023)

##      Name Age
## 1   Alice  21
## 2     Bob  22
## 3 Charlie  23
## 4   David  24

cbind(): This function combines data frames horizontally, side by side. It’s essential the data frames have the same number of rows, and the rows must have the same order. In the provided example, the first score of 91.1 corresponds with “Alice” from the first row, while the second score of 85.3 aligns with “Bob” from the second row:
```
# Create a data frame with the same number of rows
(scores_2022 <- data.frame(Score = c(91.1, 85.3)))
```
```
##   Score
## 1  91.1
## 2  85.3
```
```
# Combine data frames by columns
cbind(students_2022, scores_2022)
```
```
##    Name Age Score
## 1 Alice  21  91.1
## 2   Bob  22  85.3
```

merge(): The merge() function comes into play when data frames don’t necessarily have rows in the same order, but possess a shared identifier (such as “Name”). This function aligns the data frames by the shared identifier, determined using the by argument (such as by = "Name"):

# Create a data frame with a common column "Name"
(scores_2022 <- data.frame(Name = c("Bob", "Alice"), Score = c(85.3, 91.1)))

##    Name Score
## 1   Bob  85.3
## 2 Alice  91.1

# Merge data frames by common column "Name"
merge(students_2022, scores_2022, by = "Name")

##    Name Age Score
## 1 Alice  21  91.1
## 2   Bob  22  85.3

merge() with Different Merge Types: Sometimes, two data frames intended for merging may have varying row counts. This can occur because one data frame contains extra entries not found in the other. In these cases, you can specify the type of merge to perform:

Inner Merge (all = FALSE): Retains only the entries found in both data frames.
Outer Merge (all = TRUE): Retains all unique entries from both data frames.
Left Merge (all.x = TRUE): Keeps all entries from the first data frame, regardless of whether they have a match in the second data frame.
Right Merge (all.y = TRUE): Keeps all entries from the second data frame.

If an entry is present in one data frame but absent in the other, the missing columns for that entry are populated with NA values:

# Construct a data frame with a partially shared "Name" column
(scores_2022 <- data.frame(Name = c("Bob", "Eva"), Score = c(85.3, 78.3)))

##   Name Score
## 1  Bob  85.3
## 2  Eva  78.3

# Inner-merge retaining common 'Name' entries (benchmark)
merge(students_2022, scores_2022, by = "Name", all = FALSE)

##   Name Age Score
## 1  Bob  22  85.3

# Outer-merge retaining all unique 'Name' entries from both data frames
merge(students_2022, scores_2022, by = "Name", all = TRUE)

##    Name Age Score
## 1 Alice  21    NA
## 2   Bob  22  85.3
## 3   Eva  NA  78.3

# Left-merge to keep all rows from 'students_2022'
merge(students_2022, scores_2022, by = "Name", all.x = TRUE)

##    Name Age Score
## 1 Alice  21    NA
## 2   Bob  22  85.3

# Right-merge to retain all rows from 'scores_2022'
merge(students_2022, scores_2022, by = "Name", all.y = TRUE)

##   Name Age Score
## 1  Bob  22  85.3
## 2  Eva  NA  78.3

do.call() + rbind(), cbind(), or merge(): When you use the indirect function do.call() in combination with functions like rbind(), cbind(), or merge() and supply a list of data frames, it effectively binds them together.

For example, if you have a list of data frames and you want to bind them all together into one data frame by stacking them vertically:
```
# Create data frames for different months
jan <- data.frame(Name = c("Eve", "Frank"), Age = c(25, 26))
feb <- data.frame(Name = c("Grace", "Harry"), Age = c(27, 28))
mar <- data.frame(Name = c("Irene"), Age = c(29))

# Save all data frames in a list
list_of_dfs <- list(jan, feb, mar)

# Combine all data frames by rows
(combined_df <- do.call(rbind, list_of_dfs))
```
```
##    Name Age
## 1   Eve  25
## 2 Frank  26
## 3 Grace  27
## 4 Harry  28
## 5 Irene  29
```
What do.call() does here is similar to iteratively binding each data frame in the list. The resulting combined_df stacks jan, feb, and mar on top of each other. The advantage of utilizing do.call(rbind, list_of_dfs) over the direct rbind(jan, feb, mar) approach is its flexibility: it can merge any number of data frames within a list without needing to know their individual names or the total count. This makes do.call() particularly valuable when the number of data frames is unpredictable, a scenario frequently encountered in data repositories. In such repositories, data might be segmented into separate data frames for each year. Using the conventional rbind() method would necessitate yearly adjustments to accommodate the varying number of data frames. In contrast, the do.call() method operates smoothly without such annual adjustments.

When combining multiple data frames, always check for consistency in column names and data types to prevent unexpected results.

4.5.7 Apply Family

In R, the apply functions execute repeated operations without the need for writing explicit loops. While initially tailored for matrices, they also offer great utility with data frames. This chapter elucidates the application of the apply family on data frames.

Apply by Columns and Rows

apply(): While initially intended for matrices, apply() can be used with data frames, treating them as lists of columns. Its core function is to process a function over rows or columns:
```
# Sample data frame
df <- data.frame(a = 1:4, b = 5:8)

# Mean values across columns (resultant is a vector)
apply(X = df, MARGIN = 2, FUN = mean)
```
```
##   a   b 
## 2.5 6.5
```
lapply(): Primarily for lists, lapply() works seamlessly with data frames, which are inherently lists of vectors (columns). It processes a function over each column, producing a list:
```
# Derive mean for each column (output is a list)
lapply(X = df, FUN = mean)
```
```
## $a
## [1] 2.5
## 
## $b
## [1] 6.5
```
sapply(): A more concise form of lapply(), sapply() tries to yield a simplified output, outputting vectors, matrices, or lists based on the scenario:
```
# Determine mean for each column (output is a vector)
sapply(X = df, FUN = mean)
```
```
##   a   b 
## 2.5 6.5
```

vapply(): Resembling sapply(), with vapply() you declare the return value’s type, ensuring a uniform output:

# Derive mean for each column while stating the output type
vapply(X = df, FUN = mean, FUN.VALUE = numeric(1))

##   a   b 
## 2.5 6.5

mapply(): This is the “multivariate” version of apply. It applies a function across multiple input lists on an element-to-element basis:

# Sample data sets
df <- data.frame(x = 1:3, y = 4:6, z = 9:11)

# Apply function
with(df, mapply(FUN = function(x, y, z) (y - z)^x, x, y, z))

## [1]   -5   25 -125

Apply by Groups

When dealing with grouped or categorized data, the goal often becomes performing operations within these distinct groups rather than across entire rows or columns. Typically, a specific column in the data frame denotes these groups, categorizing each data point. R provides several functions, part of the apply family and beyond, that allow for such “group-wise” computation.

split(): Before diving into the apply-by-group functions, understanding split() is crucial. It partitions a data frame based on the levels of a factor, producing a list of data frames. This facilitates the application of functions to each subset individually.

# Sample grouped data frame
df_grouped <- data.frame(group = c("A", "A", "B", "B", "B"), 
                         value = c(10, 20, 30, 40, 50))
print(df_grouped)

##   group value
## 1     A    10
## 2     A    20
## 3     B    30
## 4     B    40
## 5     B    50

# Splitting the data frame by 'group'
split_data <- split(x = df_grouped, f = df_grouped$group)
print(split_data)

## $A
##   group value
## 1     A    10
## 2     A    20
## 
## $B
##   group value
## 3     B    30
## 4     B    40
## 5     B    50

Split-Apply-Combine strategy with split() + lapply() + do.call() + c(): The split-apply-combine strategy is foundational in R. First, data is split into subsets based on some criteria (often a factor). Next, a function is applied to each subset independently. Finally, results are combined back into a useful data structure.

# Split: Dividing the data based on 'group'
(split_data <- split(x = df_grouped$value, f = df_grouped$group))

## $A
## [1] 10 20
## 
## $B
## [1] 30 40 50

# Apply: Summing the 'value' within each split group
(applied_data <- lapply(X = split_data, FUN = sum))

## $A
## [1] 30
## 
## $B
## [1] 120

# Combine: combines results into a named vector
(combined_data <- do.call(what = c, args = applied_data))

##   A   B 
##  30 120

tapply(): The tapply() function stands for “table-apply”. It quickly implements the split-apply-combine approach, using its INDEX parameter to define the grouping.
```
# Summing 'value' based on 'group'
tapply(X = df_grouped$value, INDEX = df_grouped$group, FUN = sum)
```
```
##   A   B 
##  30 120
```
aggregate(): The aggregate() function employs the split-apply-combine approach, returning a data frame that combines group names with computed statistics for each group.
```
# Using aggregate() to compute the sum for each group
df_agg <- aggregate(x = value ~ group, 
                    data = df_grouped, 
                    FUN = sum)

# Alternative: Using aggregate() with lists
df_agg <- aggregate(x = list(value = df_grouped$value), 
                    by = list(group = df_grouped$group), 
                    FUN = sum)
print(df_agg)
```
```
##   group value
## 1     A    30
## 2     B   120
```
- The formula x = value ~ group indicates that the function should summarize the value variable based on the group variable.
- The data = df_grouped argument specifies the dataset to use.
- The FUN = sum argument tells the function to compute the sum for each group.
- Alternatively, using lists: the x argument takes a list that specifies the variables to be aggregated, and the by argument provides a list that determines how the dataset is grouped.
The result is a summary data frame where each unique level of the group variable has a corresponding sum of the value variable.

aggregate() with multiple variables: The aggregate() function can handle scenarios that involve multiple group and value variables. When you have a dataset with more than one group and value column, you can use the aggregate() function to group by multiple columns and compute summaries over several value columns simultaneously.

# Sample dataset with multiple groups and values
df_advanced <- data.frame(
    group1 = c("A", "A", "A", "B", "B", "B"),
    group2 = c("X", "X", "Y", "X", "Y", "Y"),
    v1 = c(10, 20, 30, 40, 50, 60),
    v2 = c(5, 10, 15, 20, 25, 30)
)

# Using aggregate() to compute the mean for each group1 & group2 combination
df_agg <- aggregate(x = cbind(v1, v2) ~ group1 + group2, 
                    data = df_advanced, 
                    FUN = mean)

# Alternative: Using aggregate() with lists    
df_agg <- aggregate(x = df_advanced[c("v1", "v2")], 
                    by = df_advanced[c("group1", "group2")], 
                    FUN = sum)
print(df_agg)

##   group1 group2  v1 v2
## 1      A      X  30 15
## 2      B      X  40 20
## 3      A      Y  30 15
## 4      B      Y 110 55

The formula cbind(v1, v2) ~ group1 + group2 instructs R to group by both group1 and group2, and then summarize both v1 and v2.
The data = df_advanced argument specifies the dataset to use.
The FUN = mean tells the function to calculate the mean for each grouped set of data.
In the list-based approach, the x argument provides the data columns to aggregate, while the by argument specifies the grouping columns.

The resulting output showcases the average values for v1 and v2 for each unique combination of group1 and group2. This approach offers a concise way to produce summaries for complex datasets with multiple grouping variables.

In essence, group-wise computation is a cornerstone in many analyses. Knowing how to efficiently split, process, and combine data is pivotal. Functions in R, especially within the apply family, provide the tools to handle such computations with ease, making the data analysis process streamlined and robust.

4.5.8 Reshape Data Frames

Working with different data formats is essential for a seamless data analysis experience. In R, the two primary data structures are the wide and long formats:

Wide Format: In this configuration, each row corresponds to a unique observation, with all its associated measurements or characteristics spread across distinct columns. To illustrate, consider an individual named John. In the wide format, John would occupy a single row. Attributes such as age, gender, and IQ would each have their own columns. For John, these might be represented as separate columns with values 38, Male, and 120, respectively.

Table 4.1: Wide Format Example

Name

Age

Gender

IQ

John

38

Male

120

Marie

29

Female

121

Table 4.1: Wide Format Example
Name	Age	Gender	IQ
John	38	Male	120
Marie	29	Female	121

Long Format: Contrary to the wide format, in the long format, each row stands for just one characteristic or measurement of an observation. As a result, a single entity might be represented across several rows. Using John as an example again, he would be spread across three rows, one for each attribute. The dataset would typically have three columns: one indicating the individual (John, John, John), one specifying the type of attribute (age, gender, IQ), and the last one containing the corresponding values (38, Male, 120).

Table 4.2: Long Format Example
Name	Attribute	Value
John	Age	38
John	Gender	Male
John	IQ	120
Marie	Age	29
Marie	Gender	Female
Marie	IQ	121

The reshape() function offers a robust method to toggle between these two formats.

# Sample data in wide format
wide_data <- data.frame(
    name = c("John", "Marie"),
    age = c(38, 29),
    gender = c("Male", "Female"),
    iq = c(120, 121)
)
print(wide_data)

##    name age gender  iq
## 1  John  38   Male 120
## 2 Marie  29 Female 121

# Convert to long format
long_data <- reshape(
    data = wide_data, 
    direction = "long", 
    varying = list(attribute = c("age", "gender", "iq")),
    times = c("Age", "Gender", "IQ"),
    timevar = "attribute",
    v.names = "value",
    idvar = "name"
)
rownames(long_data) <- NULL
print(long_data)

##    name attribute  value
## 1  John       Age     38
## 2 Marie       Age     29
## 3  John    Gender   Male
## 4 Marie    Gender Female
## 5  John        IQ    120
## 6 Marie        IQ    121

# Convert long format back to wide format
reshaped_wide_data <- reshape(
    data = long_data, 
    direction = "wide", 
    timevar = "attribute",
    v.names = "value",
    idvar = "name",
    sep = "_"
)
print(reshaped_wide_data)

##    name value_Age value_Gender value_IQ
## 1  John        38         Male      120
## 2 Marie        29       Female      121

In the reshape function:

data: This specifies the data frame you intend to reshape.
direction: Determines if you’re going from ‘wide’ to ‘long’ format or vice-versa.
varying: Lists columns that you’ll be reshaping.
times: This denotes unique times or measurements in the reshaped data.
timevar: This names the column in the reshaped data that will contain the unique times identifiers.
v.names: The name of the column in the reshaped data that will contain the data values.
idvar: Specifies the identifier variable, which will remain the same between reshaped versions.
sep: Used in converting from long to wide format, it defines the separator between the identifier and the measurement variables.

For beginners, the reshape() function might seem intricate due to its numerous parameters. Yet, with practice, it becomes a valuable tool in a data scientist’s toolkit. Always refer to R’s built-in documentation with ?reshape for additional details, or read the vignette available through vignette("reshape").

4.6 Tibble (`tbl_df`)

A tibble (tbl_df) refines the conventional data frame, offering a more user-friendly alternative. It is part of the tibble package by Müller and Wickham (2023), which is in the tidyverse collection of R packages (Wickham 2023c). For an introduction into the Tidyverse, consult Chapter 3.6.7.

To use tibbles, you need to install the tibble package by executing install.packages("tibble") in your console. Don’t forget to include library("tibble") at the beginning of your R script. If you’re already using the Tidyverse suite, a simple library("tidyverse") will suffice, as it internally loads the tibble package.

Despite their modern touch, tibbles remain data frames at their core. This duality is evident when the class() function, applied to a tibble, returns both "tbl_df" and "data.frame". Therefore, the operations and functions elucidated in the data frame section @ref(data.frame) are entirely compatible with tibbles.

Building on this compatibility, this chapter explores the Tidyverse way of manipulating tibbles, leveraging user-friendly functions from the dplyr package by Wickham et al. (2023), rather than solely relying on base functions. The dplyr package is one of the core packages of the tidyverse collection and specializes in data manipulation. The package offers a series of verbs (functions) for the most common data manipulation tasks. Let’s explore some of these functions and see how they can be applied to tibbles.

4.6.1 Create a Tibble

Tibbles can be formed using the tibble() function from the tibble package:

# Load tibble package
library("tibble")

# Create vectors for the tibble
names <- c("Anna", "Ella", "Sophia")
ages <- c(23, NA, 26)
female <- c(TRUE, TRUE, TRUE)
grades <- factor(c("A", "B", "A"), levels = rev(LETTERS[1:6]), ordered = TRUE)
major <- c("Math", "Biology", "Physics")

# Construct the tibble
students_tbl <- tibble(name = names, 
                       age = ages, 
                       female = female,
                       grade = grades, 
                       major = major)
print(students_tbl)

## # A tibble: 3 × 5
##   name     age female grade major  
##   <chr>  <dbl> <lgl>  <ord> <chr>  
## 1 Anna      23 TRUE   A     Math   
## 2 Ella      NA TRUE   B     Biology
## 3 Sophia    26 TRUE   A     Physics

Moreover, tibbles support incremental construction by referencing a previously established tibble and appending additional columns:

# Initiate the tibble
students_tbl <- tibble(name = names, 
                       age = ages,
                       female = female)

# Expand the tibble by adding columns
students_tbl <- tibble(students_tbl,
                       grade = grades, 
                       major = major)
print(students_tbl)

## # A tibble: 3 × 5
##   name     age female grade major  
##   <chr>  <dbl> <lgl>  <ord> <chr>  
## 1 Anna      23 TRUE   A     Math   
## 2 Ella      NA TRUE   B     Biology
## 3 Sophia    26 TRUE   A     Physics

Unlike regular data frames, tibbles allow non-standard column names. You can use special characters or numbers as column names. Here’s an example:

# Construct a tibble with unconventional column names
tibble(`:)` = "smile", 
       ` ` = "space", 
       `2000` = "number")

## # A tibble: 1 × 3
##   `:)`  ` `   `2000`
##   <chr> <chr> <chr> 
## 1 smile space number

Another way to create a tibble is with the tribble() function. It allows you to define column headings using formulas starting with ~ and separate entries with commas. Here’s an example:

tribble(
    ~x, ~y, ~z,
    "a", 2, 3.6,
    "b", 1, 8.5
)

## # A tibble: 2 × 3
##   x         y     z
##   <chr> <dbl> <dbl>
## 1 a         2   3.6
## 2 b         1   8.5

4.6.2 Inspect a Tibble

To discern the type and components of a tibble, the following functions can be employed:

# Identify the data structure of the tibble
class(students_tbl)          # Outputs "tbl_df" "tbl" "data.frame".
is_tibble(students_tbl)      # Outputs TRUE.
is.data.frame(students_tbl)  # Outputs TRUE.
is.matrix(students_tbl)      # Outputs FALSE.

## [1] "tbl_df"     "tbl"        "data.frame"
## [1] TRUE
## [1] TRUE
## [1] FALSE

# Identify the data type of each column within the tibble
sapply(students_tbl, class)

## $name
## [1] "character"
## 
## $age
## [1] "numeric"
## 
## $female
## [1] "logical"
## 
## $grade
## [1] "ordered" "factor" 
## 
## $major
## [1] "character"

Inspecting tibbles can be achieved using functions like nrow(), ncol(), dim(), head(), tail(), str(), summarize(), and View(), much like their use for data frames as outlined in Chapter 4.5.2. However, when printing a tibble in R, the default behavior differs from that of a data frame. Only the first 10 rows and the columns that fit on the screen are displayed, accompanied by a message noting the additional rows and columns present. This makes the head() and tail() functions less necessary, as printing a tibble already provides a concise overview.

For a more concise structural overview of a tibble, instead of using str(), one might prefer the glimpse() function from the tibble package:

# Examine the tibble's structure
glimpse(students_tbl)

## Rows: 3
## Columns: 5
## $ name   <chr> "Anna", "Ella", "Sophia"
## $ age    <dbl> 23, NA, 26
## $ female <lgl> TRUE, TRUE, TRUE
## $ grade  <ord> A, B, A
## $ major  <chr> "Math", "Biology", "Physics"

4.6.3 Select and Modify

The dplyr package (Wickham et al. 2023) from the Tidyverse provides an array of functions tailored for data manipulation with tibbles.

# Load the dplyr package
library("dplyr")

Select and Order Columns

Using select() to retrieve specific columns:

# Base R method
students_tbl[c("name", "grade")]

## # A tibble: 3 × 2
##   name   grade
##   <chr>  <ord>
## 1 Anna   A    
## 2 Ella   B    
## 3 Sophia A

# With dplyr
select(students_tbl, name, grade)

## # A tibble: 3 × 2
##   name   grade
##   <chr>  <ord>
## 1 Anna   A    
## 2 Ella   B    
## 3 Sophia A

Using select() to order columns alphabetically:

# Base R method
students_tbl[sort(colnames(students_tbl))]

## # A tibble: 3 × 5
##     age female grade major   name  
##   <dbl> <lgl>  <ord> <chr>   <chr> 
## 1    23 TRUE   A     Math    Anna  
## 2    NA TRUE   B     Biology Ella  
## 3    26 TRUE   A     Physics Sophia

# With dplyr
select(students_tbl, sort(colnames(students_tbl)))

## # A tibble: 3 × 5
##     age female grade major   name  
##   <dbl> <lgl>  <ord> <chr>   <chr> 
## 1    23 TRUE   A     Math    Anna  
## 2    NA TRUE   B     Biology Ella  
## 3    26 TRUE   A     Physics Sophia

Filter and Order Rows

Use filter() to extract rows based on conditions:

# Base R method
students_tbl[students_tbl$age > 24 & students_tbl$grade == "A", ]

## # A tibble: 1 × 5
##   name     age female grade major  
##   <chr>  <dbl> <lgl>  <ord> <chr>  
## 1 Sophia    26 TRUE   A     Physics

# With dplyr
filter(students_tbl, age > 24 & grade == "A")

## # A tibble: 1 × 5
##   name     age female grade major  
##   <chr>  <dbl> <lgl>  <ord> <chr>  
## 1 Sophia    26 TRUE   A     Physics

The rows can be ordered with the arrange() function:

# Base R method
students_tbl[order(students_tbl$age, decreasing = TRUE), ]

## # A tibble: 3 × 5
##   name     age female grade major  
##   <chr>  <dbl> <lgl>  <ord> <chr>  
## 1 Sophia    26 TRUE   A     Physics
## 2 Anna      23 TRUE   A     Math   
## 3 Ella      NA TRUE   B     Biology

# With dplyr
arrange(students_tbl, desc(age))

## # A tibble: 3 × 5
##   name     age female grade major  
##   <chr>  <dbl> <lgl>  <ord> <chr>  
## 1 Sophia    26 TRUE   A     Physics
## 2 Anna      23 TRUE   A     Math   
## 3 Ella      NA TRUE   B     Biology

In the dplyr approach, the desc() function is utilized to order values in descending order.

Add and Remove Columns

To create a new column, employ mutate():

# Base R method
students_tbl$gpa <- c(3.7, 3.4, 3.9)

# With dplyr
students_tbl <- mutate(students_tbl, gpa = c(3.7, 3.4, 3.9))
print(students_tbl)

## # A tibble: 3 × 6
##   name     age female grade major     gpa
##   <chr>  <dbl> <lgl>  <ord> <chr>   <dbl>
## 1 Anna      23 TRUE   A     Math      3.7
## 2 Ella      NA TRUE   B     Biology   3.4
## 3 Sophia    26 TRUE   A     Physics   3.9

Columns can be removed using select():

# Base R method
students_tbl$female <- NULL

# With dplyr
students_tbl <- select(students_tbl, -female)
print(students_tbl)

## # A tibble: 3 × 5
##   name     age grade major     gpa
##   <chr>  <dbl> <ord> <chr>   <dbl>
## 1 Anna      23 A     Math      3.7
## 2 Ella      NA B     Biology   3.4
## 3 Sophia    26 A     Physics   3.9

Manipulate Columns

To construct new values for each row based on existing columns, you can utilize the reframe() function:

# Base R method
with(students_tbl, paste0(name, " studies ", major, "."))

## [1] "Anna studies Math."      "Ella studies Biology."  
## [3] "Sophia studies Physics."

# With dplyr
reframe(students_tbl, paste0(name, " studies ", major, "."))

## # A tibble: 3 × 1
##   `paste0(name, " studies ", major, ".")`
##   <chr>                                  
## 1 Anna studies Math.                     
## 2 Ella studies Biology.                  
## 3 Sophia studies Physics.

The key difference between mutate() and reframe() is that mutate() returns the full tibble, while reframe() only returns the newly computed column:

# Using mutate() for comparison
mutate(students_tbl, new_description = paste0(name, " studies ", major, "."))

## # A tibble: 3 × 6
##   name     age grade major     gpa new_description        
##   <chr>  <dbl> <ord> <chr>   <dbl> <chr>                  
## 1 Anna      23 A     Math      3.7 Anna studies Math.     
## 2 Ella      NA B     Biology   3.4 Ella studies Biology.  
## 3 Sophia    26 A     Physics   3.9 Sophia studies Physics.

To compute summary statistics over all rows, the summarize() or summarise() function can be employed:

# Base R method
with(students_tbl, mean(gpa))

## [1] 3.666667

# With dplyr
summarize(students_tbl, mean(gpa))

## # A tibble: 1 × 1
##   `mean(gpa)`
##         <dbl>
## 1        3.67

The difference between mutate() and summarize() is that mutate() keeps the tibble format, thus, in this case, mutate() creates a new column with the average values repeated multiple times:

# Using mutate() instead of summarize()
mutate(students_tbl, mean_gpa = mean(gpa))

## # A tibble: 3 × 6
##   name     age grade major     gpa mean_gpa
##   <chr>  <dbl> <ord> <chr>   <dbl>    <dbl>
## 1 Anna      23 A     Math      3.7     3.67
## 2 Ella      NA B     Biology   3.4     3.67
## 3 Sophia    26 A     Physics   3.9     3.67

Note that while base R returns a scalar, reframe() and summarize() keep the tibble structure. To extract just the value, use the pull() function:

# Pull to retrieve a vector
pull(summarize(students_tbl, mean_gpa = mean(gpa)), mean_gpa)

## [1] 3.666667

Use the Pipe Operator

The Tidyverse introduces the pipe operator, %>%. This operator, detailed in Chapter 3.6.7, allows for sequential execution of functions:

# Without the pipe operator
mutate(select(students_tbl, -age, -grade), is_cum_laude = gpa >= 3.5)

## # A tibble: 3 × 4
##   name   major     gpa is_cum_laude
##   <chr>  <chr>   <dbl> <lgl>       
## 1 Anna   Math      3.7 TRUE        
## 2 Ella   Biology   3.4 FALSE       
## 3 Sophia Physics   3.9 TRUE

# Employ the pipe operator
students_tbl %>% 
    select(-age, -grade) %>% 
    mutate(is_cum_laude = gpa >= 3.5)

## # A tibble: 3 × 4
##   name   major     gpa is_cum_laude
##   <chr>  <chr>   <dbl> <lgl>       
## 1 Anna   Math      3.7 TRUE        
## 2 Ella   Biology   3.4 FALSE       
## 3 Sophia Physics   3.9 TRUE

With the pipe operator, operations become more readable and straightforward, promoting cleaner code structuring.

4.6.4 Add Labels

To modify the names of the columns in a tibble, you can use the rename() function from the dplyr package:

# Base R method
colnames(students_tbl) <- c("Name", "Age", "Grade", "Major", "GPA")

# With dplyr
students_tbl <- students_tbl %>% rename(Name = name,
                                        Age = age,
                                        Grade = grade,
                                        Major = major,
                                        GPA = gpa)
print(students_tbl)

## # A tibble: 3 × 5
##   Name     Age Grade Major     GPA
##   <chr>  <dbl> <ord> <chr>   <dbl>
## 1 Anna      23 A     Math      3.7
## 2 Ella      NA B     Biology   3.4
## 3 Sophia    26 A     Physics   3.9

The rename() function is particularly useful when modifying only a subset of column:

# Base R method
colnames(students_tbl)[colnames(students_tbl) == "Major"] <- "Field of Study"

# With dplyr
students_tbl <- students_tbl %>% rename(`Field of Study` = Major)
print(students_tbl)

## # A tibble: 3 × 5
##   Name     Age Grade `Field of Study`   GPA
##   <chr>  <dbl> <ord> <chr>            <dbl>
## 1 Anna      23 A     Math               3.7
## 2 Ella      NA B     Biology            3.4
## 3 Sophia    26 A     Physics            3.9

4.6.5 Handle Missing Values

Tibbles can contain missing values (NA) just like data frames. To manage these missing values, you can use the drop_na() function from the tidyr package by Wickham, Vaughan, and Girlich (2024), part of the Tidyverse.

# Load the tidyr package
library("tidyr")

# Remove all rows containing missing values
# --> Base R method
na.omit(students_tbl)

# -->  With tidyr
students_tbl %>% 
    drop_na()

## # A tibble: 2 × 5
##   Name     Age Grade `Field of Study`   GPA
##   <chr>  <dbl> <ord> <chr>            <dbl>
## 1 Anna      23 A     Math               3.7
## 2 Sophia    26 A     Physics            3.9

The drop_na() function offers the flexibility to target specific columns for NA checking, e.g. drop_na(Age), ensuring that less critical columns with numerous NA values don’t substantially reduce the dataset. For more details, consult the function documentation by executing ?drop_na.

To replace missing values, you can use functions from the dplyr package:

# Replace missing 'Age' values with mean age
# --> Base R method
students_tbl$Age[is.na(students_tbl$Age)] <- mean(students_tbl$Age, na.rm = TRUE)

# --> With dplyr
students_tbl <- students_tbl %>% 
    mutate(mean_age = mean(students_tbl$Age, na.rm = TRUE)) %>% 
    mutate(Age = ifelse(is.na(Age), mean_age, Age)) %>%
    select(-mean_age)
print(students_tbl)

## # A tibble: 3 × 5
##   Name     Age Grade `Field of Study`   GPA
##   <chr>  <dbl> <ord> <chr>            <dbl>
## 1 Anna    23   A     Math               3.7
## 2 Ella    24.5 B     Biology            3.4
## 3 Sophia  26   A     Physics            3.9

Here, the mutate() function replaces NA values in the ‘Age’ column with the mean age, calculated with na.rm = TRUE to ignore NAs in the calculation.

4.6.6 Combine Tibbles

When dealing with multiple tibbles, the Tidyverse provides powerful tools for combination and merging. Specifically, the dplyr package by Wickham et al. (2023) offers functions such as bind_rows(), bind_cols(), and various *_join() methods like inner_join(). Additionally, the purrr package by Wickham and Henry (2023) introduces the map_*() functions, including map_dfr(). Here’s how they work:

bind_rows(): This function is the Tidyverse equivalent of rbind() and stacks tibbles vertically. It requires that the columns have matching names:

# Create tibbles with identical column names
(students_2022 <- tibble(Name = c("Alice", "Bob"), Age = c(21, 22)))
(students_2023 <- tibble(Name = c("Charlie", "David"), Age = c(23, 24)))

## # A tibble: 2 × 2
##   Name    Age
##   <chr> <dbl>
## 1 Alice    21
## 2 Bob      22
## # A tibble: 2 × 2
##   Name      Age
##   <chr>   <dbl>
## 1 Charlie    23
## 2 David      24

# Combine tibbles by rows
bind_rows(students_2022, students_2023)

## # A tibble: 4 × 2
##   Name      Age
##   <chr>   <dbl>
## 1 Alice      21
## 2 Bob        22
## 3 Charlie    23
## 4 David      24

bind_cols(): This function is the Tidyverse equivalent of cbind() and aligns tibbles horizontally. Ensure the tibbles have the same number of rows:

# Create a tibble with the same number of rows
(scores_2022 <- tibble(Score = c(91.1, 85.3)))

## # A tibble: 2 × 1
##   Score
##   <dbl>
## 1  91.1
## 2  85.3

# Combine tibbles by columns
bind_cols(students_2022, scores_2022)

## # A tibble: 2 × 3
##   Name    Age Score
##   <chr> <dbl> <dbl>
## 1 Alice    21  91.1
## 2 Bob      22  85.3

inner_join(): Similar to merge(), inner_join() matches tibbles based on a shared identifier specified by the by argument:

# Create a tibble with a common column "Name"
(scores_2022 <- tibble(Name = c("Bob", "Alice"), Score = c(85.3, 91.1)))

## # A tibble: 2 × 2
##   Name  Score
##   <chr> <dbl>
## 1 Bob    85.3
## 2 Alice  91.1

# Merge tibbles by common column "Name"
inner_join(students_2022, scores_2022, by = "Name")

## # A tibble: 2 × 3
##   Name    Age Score
##   <chr> <dbl> <dbl>
## 1 Alice    21  91.1
## 2 Bob      22  85.3

Different Types of Joins with dplyr: With dplyr, there are specialized functions for each type of merge/join operation, making it more intuitive:

Inner Join: Retained entries are only those found in both tibbles.
Full (Outer) Join: Keeps all entries from both tibbles.
Left Join: Keeps all entries from the first tibble.
Right Join: Retains all entries from the second tibble.

When an entry exists in one tibble but not the other, the missing columns for that entry will be filled with NA values:

# Construct a tibble with a partially shared "Name" column
(scores_2022 <- tibble(Name = c("Bob", "Eva"), Score = c(85.3, 78.3)))

## # A tibble: 2 × 2
##   Name  Score
##   <chr> <dbl>
## 1 Bob    85.3
## 2 Eva    78.3

# Inner join to keep common 'Name' entries
inner_join(students_2022, scores_2022, by = "Name")

## # A tibble: 1 × 3
##   Name    Age Score
##   <chr> <dbl> <dbl>
## 1 Bob      22  85.3

# Full (outer) join to retain all unique 'Name' entries from both tibbles
full_join(students_2022, scores_2022, by = "Name")

## # A tibble: 3 × 3
##   Name    Age Score
##   <chr> <dbl> <dbl>
## 1 Alice    21  NA  
## 2 Bob      22  85.3
## 3 Eva      NA  78.3

# Left join to keep all rows from 'students_2022'
left_join(students_2022, scores_2022, by = "Name")

## # A tibble: 2 × 3
##   Name    Age Score
##   <chr> <dbl> <dbl>
## 1 Alice    21  NA  
## 2 Bob      22  85.3

# Right join to keep all rows from 'scores_2022'
right_join(students_2022, scores_2022, by = "Name")

## # A tibble: 2 × 3
##   Name    Age Score
##   <chr> <dbl> <dbl>
## 1 Bob      22  85.3
## 2 Eva      NA  78.3

map_dfr() and map_dfc(): For combining multiple tibbles stored in a list, the purrr package provides the map_dfr() and map_dfc() functions, which are more flexible alternatives to using do.call() in combination with rbind(), or cbind():
```
# Load purrr package
library("purrr")

# Create tibbles for different months
jan <- tibble(Name = c("Eve", "Frank"), Age = c(25, 26))
feb <- tibble(Name = c("Grace", "Harry"), Age = c(27, 28))
mar <- tibble(Name = c("Irene"), Age = c(29))

# Store all tibbles in a list
list_of_tibbles <- list(jan, feb, mar)

# Combine all tibbles by rows
(combined_tibble <- map_dfr(.x = list_of_tibbles, .f = ~.x))
```
```
## # A tibble: 5 × 2
##   Name    Age
##   <chr> <dbl>
## 1 Eve      25
## 2 Frank    26
## 3 Grace    27
## 4 Harry    28
## 5 Irene    29
```
With this approach, map_dfr() sequentially combines each tibble in the list by rows. This method is particularly useful when the number of tibbles to be combined is unknown or variable, offering more flexibility than calling functions like bind_rows(jan, feb, mar) directly. The map_dfc() function operates similarly but combines the tibbles column-wise instead of row-wise.

Within the map_*() functions, the argument .f = ~.x is a shorthand formula notation which translates to .f = function(x) x. This means that for each tibble in the list, the function takes the tibble as it is and returns it without any transformation, making it an efficient way to combine them row- or column-wise.

reduce() + *_join(): When tasked with merging multiple tibbles stored in a list based on a common column, the combination of purrr::reduce() and dplyr::*_join() functions such as dplyr::full_join() offers a more flexible alternative to using do.call() in combination with merge():

# Construct a tibble with a partially shared "Name" column
(subject_2022 <- tibble(Name = c("Bob", "Pete"), 
                        Subject = c("History", "Economics")))

## # A tibble: 2 × 2
##   Name  Subject  
##   <chr> <chr>    
## 1 Bob   History  
## 2 Pete  Economics

# A list comprising the tibbles to be merged
list_of_tibbles <- list(students_2022, scores_2022, subject_2022)

# Execute an outer-merge using reduce() and full_join()
(merged_tibble <- reduce(list_of_tibbles, .f = ~full_join(.x, .y, by = "Name")))

## # A tibble: 4 × 4
##   Name    Age Score Subject  
##   <chr> <dbl> <dbl> <chr>    
## 1 Alice    21  NA   <NA>     
## 2 Bob      22  85.3 History  
## 3 Eva      NA  78.3 <NA>     
## 4 Pete     NA  NA   Economics

4.6.7 Apply Family

In R, the Tidyverse collection of packages offers functions for manipulating tibbles in a more readable and consistent manner. This chapter focuses on these functionalities that replace the traditional apply family used with data frames.

Apply by Columns and Rows

map(): Instead of apply(), use the purrr::map() function to process each column of a tibble:

# Sample tibble
tb <- tibble(a = 1:4, b = 5:8)

# Mean values across columns (resultant is a list)
map(tb, mean)

## $a
## [1] 2.5
## 
## $b
## [1] 6.5

map_dbl(): Similar to lapply(), the purrr::map_dbl() function processes each column and returns a double vector:
```
# Mean values for each column (output is a double vector)
map_dbl(tb, mean)
```
```
##   a   b 
## 2.5 6.5
```

Apply by Groups

When dealing with grouped data, you can perform operations within these distinct groups using Tidyverse functions.

group_by() + summarize(): This pair of functions from dplyr replaces the need for split() and lapply():

# Sample grouped tibble
tb_grouped <- tibble(group = c("A", "A", "B", "B", "B"), 
                     value = c(10, 20, 30, 40, 50))

# Summarizing 'value' based on 'group'
tb_grouped %>% 
    group_by(group) %>% 
    summarize(sum_value = sum(value))

## # A tibble: 2 × 2
##   group sum_value
##   <chr>     <dbl>
## 1 A            30
## 2 B           120

group_by() + summarize() for Multiple Groups and Variables: The dplyr functions can handle multiple group and value variables:

# Sample tibble with multiple groups and values
tb_advanced <- tibble(
    group1 = c("A", "A", "A", "B", "B", "B"),
    group2 = c("X", "X", "Y", "X", "Y", "Y"),
    v1 = c(10, 20, 30, 40, 50, 60),
    v2 = c(5, 10, 15, 20, 25, 30)
)

# Summarize for each group1 & group2 combination
tb_advanced %>% 
    group_by(group1, group2) %>% 
    summarize(mean_v1 = mean(v1), 
              mean_v2 = mean(v2))

## # A tibble: 4 × 4
## # Groups:   group1 [2]
##   group1 group2 mean_v1 mean_v2
##   <chr>  <chr>    <dbl>   <dbl>
## 1 A      X           15     7.5
## 2 A      Y           30    15  
## 3 B      X           40    20  
## 4 B      Y           55    27.5

4.6.8 Reshape Tibbles

As discussed in Chapter 4.5.8, data can be organized in either a wide or long format:

Wide Format: The wide format has each row representing a unique observation, with various attributes detailed across columns.
Long Format: Contrary to the wide format, the long format has each row representing a single attribute or measure of an observation, resulting in multiple rows for each observation.

The tidyr package by Wickham, Vaughan, and Girlich (2024) provides two key functions for reshaping data: pivot_longer() and pivot_wider():

# Load tidyr package
library("tidyr")

# Create tibble using wide format
wide_data <- tibble(
    Name = c("John", "Marie"),
    Age = c(38, 29),
    Gender = c("Male", "Female"),
    IQ = c(120, 121)
)
print(wide_data)

## # A tibble: 2 × 4
##   Name    Age Gender    IQ
##   <chr> <dbl> <chr>  <dbl>
## 1 John     38 Male     120
## 2 Marie    29 Female   121

# Coerce all varying attributes to character type
wide_data <- wide_data %>% 
    mutate(across(where(is.numeric), as.character))

# Pivot to long format
long_data <- wide_data %>% 
    pivot_longer(cols = -Name, 
                 names_to = "Attribute", 
                 values_to = "Value")
print(long_data)

## # A tibble: 6 × 3
##   Name  Attribute Value 
##   <chr> <chr>     <chr> 
## 1 John  Age       38    
## 2 John  Gender    Male  
## 3 John  IQ        120   
## 4 Marie Age       29    
## 5 Marie Gender    Female
## 6 Marie IQ        121

# Convert long format back to wide format
reshaped_wide_data <- long_data %>% 
    pivot_wider(names_from = Attribute, 
                values_from = Value)
print(reshaped_wide_data)

## # A tibble: 2 × 4
##   Name  Age   Gender IQ   
##   <chr> <chr> <chr>  <chr>
## 1 John  38    Male   120  
## 2 Marie 29    Female 121

In pivot_longer() and pivot_wider():

cols: Specifies the columns to pivot into longer or wider format.
names_to: Names the column in the reshaped data containing the unique identifiers.
values_to: Names the column in the reshaped data that will hold the data values.
names_from: Indicates the column that will provide names in the widened data.
values_from: Indicates the column that will provide values in the widened data.

For those new to tibbles and tidyverse, these functions may initially seem complicated. However, they offer a straightforward way to reshape data in R. You can always refer to the official documentation (?pivot_longer, ?pivot_wider) or read available vignettes for further insights.

4.7 Data Table (`data.table`)

A data table (data.table) is similar to a data frame but with more advanced features for data manipulation. Credited to the data.table package by Barrett et al. (2024), data tables are known for their high-speed operations, particularly beneficial for large datasets. This sets them apart from tibbles which, although more user-friendly, may not be as optimized for speed. Consequently, data.table and tibble can be seen as competitors, each improving upon the basic data frame in their unique ways. Like tibble, data.table is not a part of base R. It requires the installation of the data.table package via install.packages("data.table"), followed by library("data.table") at the beginning of your script.

The syntax of data.table differs significantly from the syntax used in the Tidyverse, making the R codes appear almost as distinct languages. While my research often employs data.table for its efficiency, in this book, I have chosen to emphasize tibble and the associated Tidyverse syntax. This decision is primarily due to the more intuitive and user-friendly nature of the Tidyverse.

For those who wish to explore the data.table package in more depth, I suggest starting with its vignette. You can access it in R using:

vignette("datatable-intro", package = "data.table")

If you’re unsure about the specific vignettes available, list all vignettes associated with data.table:

vignette(package = "data.table")

Then, based on your interest, you can select a vignette and view it with the vignette() function, as shown earlier.

Moreover, for structured learning on data.table, DataCamp offers comprehensive courses including:

These courses provide an in-depth exploration, from basic operations to advanced manipulations using data.table.

4.8 Extensible Time Series (`xts`)

The extensible time series (xts) object of the xts package by Ryan and Ulrich (2024b) pairs a matrix with a time index:

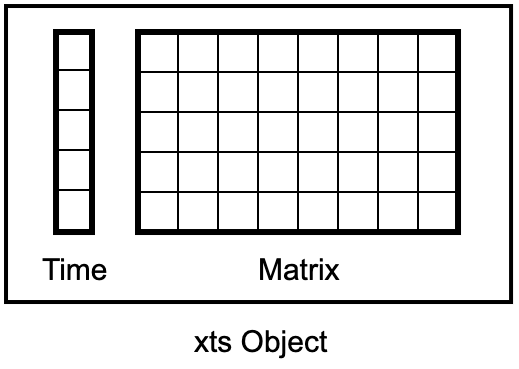
Figure 4.1: xts Object as a Matrix with Time Index

In xts, each row of a matrix is marked with a unique timestamp, typically formatted as a Date or POSIXct. Details on creating Date or POSIXct time indices can be gathered from Chapter 3.3. It’s important to note that an xts object’s base is a matrix, not a data frame or tibble, which mandates that all columns share the same data type. This means an xts object contains exclusively numbers or characters but not a mix of the two. While most matrix-related functions from Chapter 4.3 are compatible with xts objects, xts offers an additional set of specialized functions tailored for handling time series data.

By design, xts objects always sort data chronologically, from the earliest to the latest observation. If you have use-cases that demand arranging time series data based on other criteria (e.g., size of stock returns), it’s necessary to first revert the xts object back to a matrix or a data frame.

xts objects are fundamentally based on zoo objects from the zoo package by Zeileis, Grothendieck, and Ryan (2023), named after Zeileis’ ordered observations. These, too, are time-indexed data structures, but the xts package introduces additional functionalities.

To integrate xts into your workflow, it needs to be installed first using install.packages("xts"). Subsequently, invoking library("xts") at the beginning of your script loads the package.

4.8.1 Create an `xts` Object

An xts object can be created using the xts() function. This function binds data with its respective time index (order.by = time_index):

# Load xts package
library("xts")

# Create a data matrix
data <- matrix(1:12, ncol = 2, dimnames = list(NULL, c("a", "b")))
print(data)

##      a  b
## [1,] 1  7
## [2,] 2  8
## [3,] 3  9
## [4,] 4 10
## [5,] 5 11
## [6,] 6 12

# Create a time index of the same length as the data matrix
time_index <- seq(as.Date("1995-11-01"), as.Date("1996-04-01"), by = "month")
print(time_index)

## [1] "1995-11-01" "1995-12-01" "1996-01-01" "1996-02-01" "1996-03-01"
## [6] "1996-04-01"

# Create an xts object based on the data matrix its time index
dxts <- xts(x = data, order.by = time_index)
print(dxts)

##            a  b
## 1995-11-01 1  7
## 1995-12-01 2  8
## 1996-01-01 3  9
## 1996-02-01 4 10
## 1996-03-01 5 11
## 1996-04-01 6 12

4.8.2 Inspect an `xts` Object

Before delving into the specifics of an xts object, it’s helpful to grasp its overall structure and the type of time index it utilizes.

# Check data structure and time index type
class(dxts)            # Returns "xts" and "zoo", but it's also a "matrix".
typeof(dxts)           # Returns "integer".
tclass(dxts)           # Returns "Date".
is.xts(dxts)           # Returns TRUE.
is.zoo(dxts)           # Returns TRUE.
is.matrix(dxts)        # Returns TRUE.
is.data.frame(dxts)    # Returns FALSE.

## [1] "xts" "zoo"
## [1] "integer"
## [1] "Date"
## [1] TRUE
## [1] TRUE
## [1] TRUE
## [1] FALSE

To inspect xts objects, functions like nrow(), ncol(), dim(), head(), tail(), summarize(), and View() can be employed. Their application is identical to their use with matrices, as detailed in Chapter 4.3.2.

Sometimes you might want to separately view the core data (matrix) and the associated time index (Date or POSIXct vector):

# Extract the time index from the xts object
index(dxts)

## [1] "1995-11-01" "1995-12-01" "1996-01-01" "1996-02-01" "1996-03-01"
## [6] "1996-04-01"

# Retrieve the core data as a matrix from the xts object
coredata(dxts)

##      a  b
## [1,] 1  7
## [2,] 2  8
## [3,] 3  9
## [4,] 4 10
## [5,] 5 11
## [6,] 6 12

# Retrieve the core data as a numeric vector from the xts object
as.numeric(dxts)

##  [1]  1  2  3  4  5  6  7  8  9 10 11 12

The xts package provides a range of functions tailored for extracting detailed information about the time index:

# Extract specific time index information
cbind(Date = index(dxts),
      Year = 1900 + .indexyear(dxts),      # -> format(index(dxts), "%Y")
      Month = 1 + .indexmon(dxts),         # -> format(index(dxts), "%m")
      Weekday = .indexwday(dxts),          # -> format(index(dxts), "%u")
      Day_by_Month = .indexmday(dxts),     # -> format(index(dxts), "%d")
      Day_by_Year = 1 + .indexyday(dxts),  # -> format(index(dxts), "%j")
      Unix_Seconds = .index(dxts),         # -> as.numeric(index(dxts)) * 86400
      Unix_Days = .index(dxts) / 86400)    # -> as.numeric(index(dxts))

##      Date Year Month Weekday Day_by_Month Day_by_Year Unix_Seconds Unix_Days
## [1,] 9435 1995    11       3            1         305    815184000      9435
## [2,] 9465 1995    12       5            1         335    817776000      9465
## [3,] 9496 1996     1       1            1           1    820454400      9496
## [4,] 9527 1996     2       4            1          32    823132800      9527
## [5,] 9556 1996     3       5            1          61    825638400      9556
## [6,] 9587 1996     4       1            1          92    828316800      9587

For a deeper understanding of Unix time and date-time formatting strings such as %Y, %m, %u, etc., please refer to Chapter 3.3. Here’s how to convert between Unix time and date format:

# Unix time conversions
all(index(dxts) == as.Date(as.numeric(index(dxts))))
all(index(dxts) == as.Date(as.POSIXct(.index(dxts))))

## [1] TRUE
## [1] TRUE

When analyzing time series data, recognizing the periodicity, frequency, and data span is crucial. The xts package offers a set of functions specifically designed for these tasks:

# Determine the start and end date of the series
start(dxts)
end(dxts)

## [1] "1995-11-01"
## [1] "1996-04-01"

# Detect the underlying frequency of the data
periodicity(dxts)

## Monthly periodicity from 1995-11-01 to 1996-04-01

# Gauge the time span covered by the data
c(y = nyears(dxts), q = nquarters(dxts), m = nmonths(dxts),
  w = nweeks(dxts), d = ndays(dxts), H = nhours(dxts),
  M = nminutes(dxts), S = nseconds(dxts))

## y q m w d H M S 
## 2 3 6 6 6 6 6 6

4.8.3 Select and Modify

One major strength of xts objects is the intuitive syntax for time subsetting. The following showcases various methods to subset data based on its Date format timestamp:

# Examples of time subsetting:
dxts["1995"]                               # All data from the year 1995

##            a b
## 1995-11-01 1 7
## 1995-12-01 2 8

dxts["1995-12-01"]                         # All data from Dec 1, 1995
dxts["1994/1996"]                          # Data from 1994 through 1996
dxts["1995-02-22/1998-08-03"]              # Data from Feb 22, 1995, to Aug 3, 1998
dxts["1996-01/03"]                         # Data from Jan through Mar 1996
dxts["1995-12/"]                           # Data from Dec 1995 to the end
xts::first(dxts, 3)                        # First three observations
xts::last(dxts, "4 months")                # Data from the last four months
xts::first(
    xts::last(dxts, "1 year"), "2 months") # First 2 months of the last year

The function xts::first() specifically references the first() function from the xts package. This is essential because both dplyr and xts have a function named first(). Since we’ve loaded dplyr earlier, using just first() would call the dplyr::first() version. By prefixing with xts::, we ensure we’re using the function from the xts package.

Because xts objects are built upon matrices, the selection and modification procedures described in Chapter 4.3.3 can also be employed with xts objects:

# Retrieve the element from the 2nd row and 1st column
dxts[2, 1]

##            a
## 1995-12-01 2

# Two approaches to update the aforementioned element to 100
dxts[2, 1] <- 100
dxts["1995-12-01", "a"] <- 100

4.8.4 Add Labels

While column names in xts objects can be modified similarly to matrices, as detailed in Chapter 4.3.4, xts objects don’t support row names. This is because the rows inherently have a time index.

# Fetching column names
colnames(dxts)

## [1] "a" "b"

# Altering column names
colnames(dxts) <- c("A", "B")
print(dxts)

##              A  B
## 1995-11-01   1  7
## 1995-12-01 100  8
## 1996-01-01   3  9
## 1996-02-01   4 10
## 1996-03-01   5 11
## 1996-04-01   6 12

4.8.5 Handle Missing Values

Given the time-dependent nature of xts objects, specific strategies can be employed to address missing values in the data. Below are some common functions and their use-cases:

na.omit(): Removes any rows containing NA values, effectively shrinking the dataset.
na.trim(): Eliminates rows with NA values only at the beginning and end of the dataset, preserving the central portion.
na.fill(): This function replaces NA entries with a specified value, for example, 666.
na.locf(): Stands for “Last Observation Carried Forward.” If an NA value is encountered, this function fills it with the previous non-missing value.
na.locf(, fromLast = TRUE): A variation of the above, but instead of using the previous value, it utilizes the subsequent non-missing value for filling.
na.approx(): Replaces NA values with linearly interpolated values, which can be particularly useful when data points are missing at regular intervals.

# Create an xts object with missing values
date_seq <- as.Date("2000-11-03") + 0:3
values <- c(3.5, NA, 4.5, NA)
dxts <- xts(x = values, order.by = date_seq)

# Different methods to handle missing values
locf <- na.locf(dxts)
locf_fromLast <- na.locf(dxts, fromLast = TRUE)
filled <- na.fill(dxts, fill = 666)
interpolated <- na.approx(dxts)

# Merging for comparison
merge(dxts, locf, locf_fromLast, filled, interpolated)

##            dxts locf locf_fromLast filled interpolated
## 2000-11-03  3.5  3.5           3.5    3.5          3.5
## 2000-11-04   NA  3.5           4.5  666.0          4.0
## 2000-11-05  4.5  4.5           4.5    4.5          4.5
## 2000-11-06   NA  4.5            NA  666.0           NA

4.8.6 Combine xts Objects

In the realm of time series analysis using R, combining multiple datasets becomes a common requirement. With xts objects, merging data according to the time index is elegantly handled by the merge() function. Notably, when you apply the merge() function to xts objects, R smartly invokes the merge.xts() function. This specialized function considers the chronological order of time indices and merges the data accordingly, eliminating the need for an explicit by argument, which one might use when dealing with matrices.

Here’s a simple demonstration:

# Sample xts objects with different time indices
xts_a <- xts(x = 1:3, 
             order.by = as.Date(c("2022-01-01", "2022-01-02", "2022-01-04")))
xts_b <- xts(x = 4:6, 
             order.by = as.Date(c("2022-01-01", "2022-01-03", "2022-01-04")))

# Merging the xts objects
merge(xts_a, xts_b)

##            xts_a xts_b
## 2022-01-01     1     4
## 2022-01-02     2    NA
## 2022-01-03    NA     5
## 2022-01-04     3     6

For situations where a variable amount of xts objects need to be combined, the Reduce() function offers a flexible solution:

# Create an additional xts object with slightly different time indices
xts_c <- xts(x = 7:9, order.by = as.Date('2022-01-04') + 0:2)

# Use Reduce with merge function to combine multiple xts objects
Reduce(f = merge, x = list(xts_a, xts_b, xts_c))

##            init x..i.. x..i...1
## 2022-01-01    1      4       NA
## 2022-01-02    2     NA       NA
## 2022-01-03   NA      5       NA
## 2022-01-04    3      6        7
## 2022-01-05   NA     NA        8
## 2022-01-06   NA     NA        9

To combine xts objects in a manner analogous to rbind() with matrices, you’d append one time series dataset after another. This approach is especially handy when consecutively adding datasets—for instance, appending data for 2023 after 2022:

# Construct xts data for 2022 and 2023
xts_2022 <- xts(1:3, order.by = as.Date('2022-01-01') + 0:2)
xts_2023 <- xts(4:6, order.by = as.Date('2023-01-01') + 0:2)

# Combine the two xts objects
combined_xts <- rbind(xts_2022, xts_2023)
print(combined_xts)

##            [,1]
## 2022-01-01    1
## 2022-01-02    2
## 2022-01-03    3
## 2023-01-01    4
## 2023-01-02    5
## 2023-01-03    6

However, a word of caution with rbind(): Ensure the time indices don’t overlap. Unlike merge(), which handles overlaps gracefully, rbind() can result in duplicated entries if there’s an overlap.

Align Time Indices

Sometimes, the time indices of two xts objects don’t match. For example, one dataset could have dates representing the start of a month, while another dataset might use the month’s end. In such situations, alignment functions such as as.yearmon() and as.yearqtr() from the zoo package can be invaluable. These functions effectively transform dates, making them represent a generalized month or quarter, regardless of the specific day:

# Convert daily dates to generalized monthly dates
xts_start <- xts(1:3, order.by = as.Date(c("2022-01-01", "2022-02-01", "2022-03-01")))
xts_end <- xts(4:6, order.by = as.Date(c("2022-01-31", "2022-02-28", "2022-03-31")))

# Merge unaligned datasets
merge(xts_start, xts_end)

##            xts_start xts_end
## 2022-01-01         1      NA
## 2022-01-31        NA       4
## 2022-02-01         2      NA
## 2022-02-28        NA       5
## 2022-03-01         3      NA
## 2022-03-31        NA       6

# Aligned time indices
index(xts_start) <- as.yearmon(index(xts_start))
index(xts_end) <- as.yearmon(index(xts_end))

# Merge the aligned datasets
merge(xts_start, xts_end)

##          xts_start xts_end
## Jan 2022         1       4
## Feb 2022         2       5
## Mar 2022         3       6

Such alignment is instrumental in ensuring datasets are combined correctly and without introducing unintended NA values.

In conclusion, the xts package, with its suite of functions and compatibility with other packages like zoo, offers comprehensive tools for efficiently combining and managing time series data in R.

4.8.7 Time Series Transformations

In the realm of time series analysis, certain operations are quintessential for processing and deducing meaningful insights. The xts package provides a rich set of tools to facilitate these transformations, such as lagging time series, computing differences, and calculating returns.

Lag Time Series

Lagging, in time series terminology, refers to the shifting of data by a specified number of periods. This is useful for comparing values across different points in time.

The lag() function shifts the data by k periods. However, it’s essential to note that lag() is a wrapper function: its behavior adapts based on the object type. For xts objects, lag() internally calls lag.xts(). Additionally, various other packages such as dplyr also include a function called lag(), potentially leading to confusion. Therefore, for xts objects, the direct use of lag.xts() is advised.

To elucidate, here’s a sample xts object:

# Define an xts object
dxts <- xts(c(100, 102, 103, 101, 108), order.by = as.Date("2022-01-01") + 0:4)

Notice that when we introduce a one-period lag to the data, the initial value 100 from the original series aligns with the subsequent date 2022-01-02 in the lagged series. This indicates that, as of 2022-01-02, the value 100 is a lagged observation as it pertains to the previous period:

# Implement a single-period lag
lagged_data <- lag.xts(dxts, k = 1)
print(lagged_data)

##            [,1]
## 2022-01-01   NA
## 2022-01-02  100
## 2022-01-03  102
## 2022-01-04  103
## 2022-01-05  101

# Comparison: original vs. lagged data
merge(dxts, lagged_data)

##            dxts lagged_data
## 2022-01-01  100          NA
## 2022-01-02  102         100
## 2022-01-03  103         102
## 2022-01-04  101         103
## 2022-01-05  108         101

If the intent is to lag the data by two periods, the operation would be:

# Shift data two periods forward
lagged_data_two <- lag.xts(dxts, k = 2)
print(lagged_data_two)

##            [,1]
## 2022-01-01   NA
## 2022-01-02   NA
## 2022-01-03  100
## 2022-01-04  102
## 2022-01-05  103

# Comparison: original and doubly-lagged data
merge(dxts, lagged_data_two)

##            dxts lagged_data_two
## 2022-01-01  100              NA
## 2022-01-02  102              NA
## 2022-01-03  103             100
## 2022-01-04  101             102
## 2022-01-05  108             103

Should you wish to remove the initial NA values, the command transforms slightly:

# Forward shift by two periods, excluding initial NAs
lagged_trimmed <- lag.xts(dxts, k = 2, na.pad = FALSE)
print(lagged_trimmed)

##            [,1]
## 2022-01-03  100
## 2022-01-04  102
## 2022-01-05  103

Intriguingly, the k parameter is flexible enough to process negative values (which leads the series) or even vector inputs. The latter results in a matrix output where each column stands for a different lag duration:

# Various lag periods applied to data
various_lags <- lag.xts(dxts, k = -2:2)
print(various_lags)

##            lag.2 lag.1 lag0 lag1 lag2
## 2022-01-01   103   102  100   NA   NA
## 2022-01-02   101   103  102  100   NA
## 2022-01-03   108   101  103  102  100
## 2022-01-04    NA   108  101  103  102
## 2022-01-05    NA    NA  108  101  103

In the realm of time series analysis, the ability to lag proves indispensable. For instance, discerning the correlation between the present and lagged values can be insightful in gauging the persistence or autocorrelation of a time series:

# Compute time series persistence
cor(lag.xts(dxts, k = 0:1), use = "complete.obs")[1,2]

## [1] -0.3321819

Convert Levels to Changes

A critical step in the analysis of economic and financial time series is the conversion of time series levels into changes or differences. For instance, discerning a change in the unemployment rate can offer insights about the economy’s trajectory.

To undertake this, the diff() function computes these differences. But, as with the lag function, it’s safer to use diff.xts().

Comparing the outputs of diff.xts() and lag.xts():

# Compute first difference with both diff.xts() and lag.xts()
first_diff <- diff.xts(dxts)
first_diff_alt <- dxts - lag.xts(dxts)

# Comparison: original data vs. computed differences
merge(dxts, first_diff, first_diff_alt)

##            dxts first_diff first_diff_alt
## 2022-01-01  100         NA             NA
## 2022-01-02  102          2              2
## 2022-01-03  103          1              1
## 2022-01-04  101         -2             -2
## 2022-01-05  108          7              7

To compute differences relative to two periods prior:

# Derive difference considering two preceding periods
first_diff_two <- diff.xts(dxts, lag = 2)
first_diff_two_alt <- dxts - lag.xts(dxts, k = 2)

# Comparison: original data with two-period differences
merge(dxts, first_diff_two, first_diff_two_alt)

##            dxts first_diff_two first_diff_two_alt
## 2022-01-01  100             NA                 NA
## 2022-01-02  102             NA                 NA
## 2022-01-03  103              3                  3
## 2022-01-04  101             -1                 -1
## 2022-01-05  108              5                  5

The second difference is the difference of the first difference:

# Compute the second difference
second_diff <- diff.xts(dxts, differences = 2)
second_diff_alt <- (first_diff - lag.xts(first_diff, k = 1))

# Comparison: original, first-differenced, and second-differenced data
merge(dxts, first_diff, second_diff, second_diff_alt)

##            dxts first_diff second_diff second_diff_alt
## 2022-01-01  100         NA          NA              NA
## 2022-01-02  102          2          NA              NA
## 2022-01-03  103          1          -1              -1
## 2022-01-04  101         -2          -3              -3
## 2022-01-05  108          7           9               9

For those analyzing financial and economic time series, growth rates offer a lens into relative changes over time. For instance, GDP growth rates provide insights into economic progression:

# Calculate growth rates in percent
growth_rate <- 100 * diff.xts(dxts) / lag.xts(dxts, k = 1)
growth_rate_alt <- 100 * (dxts - lag.xts(dxts, k = 1)) / lag.xts(dxts, k = 1)

# Comparison: original data and computed growth rates
merge(dxts, growth_rate, growth_rate_alt)

##            dxts growth_rate growth_rate_alt
## 2022-01-01  100          NA              NA
## 2022-01-02  102   2.0000000       2.0000000
## 2022-01-03  103   0.9803922       0.9803922
## 2022-01-04  101  -1.9417476      -1.9417476
## 2022-01-05  108   6.9306931       6.9306931

Additionally, log differences are pivotal for financial and economic series. They approximate growth rates when they hover around smaller values (e.g., within $\pm 20\%$):

# Derive log differences in percent
log_diff <- 100 * diff.xts(dxts, log = TRUE)
log_diff_alt <- 100 * (log(dxts) - lag.xts(log(dxts), k = 1))

# Comparison: original data, growth rates, and log differences
merge(dxts, growth_rate, log_diff, log_diff_alt)

##            dxts growth_rate   log_diff log_diff_alt
## 2022-01-01  100          NA         NA           NA
## 2022-01-02  102   2.0000000  1.9802627    1.9802627
## 2022-01-03  103   0.9803922  0.9756175    0.9756175
## 2022-01-04  101  -1.9417476 -1.9608471   -1.9608471
## 2022-01-05  108   6.9306931  6.7010710    6.7010710

Make Time Series Regular

In time series data, especially in financial datasets, you might find datasets with irregular intervals between observations. For example, daily yield data might exclude weekends and public holidays. Such irregularities can complicate analyses that assume regular intervals. When using functions like lag.xts() and diff.xts() that relate the current with the previous period, the span of a single “lag” can vary, sometimes representing a day or even an entire week. Consequently, interpretations of differences or growth rates can be skewed, as they might be influenced by these varying intervals.

Example of an irregular monthly time series:

# Define an irregular monthly time series
xts_irregular <- xts(x = 1:4, order.by = as.Date(c("2022-01-01", "2022-02-01", 
                                                   "2022-05-01", "2022-07-01")))
print(xts_irregular)

##            [,1]
## 2022-01-01    1
## 2022-02-01    2
## 2022-05-01    3
## 2022-07-01    4

To standardize these intervals, a common approach in the xts universe involves merging the irregular data with an xts object that has a regular frequency. Here’s how you can achieve this:

Creating a Regular Time Index: Firstly, create a sequence of dates with regular intervals, covering the entire span of your irregular dataset.

# Creating a daily sequence from the start to the end of your irregular data
regular_time <- seq(from = start(xts_irregular), 
                    to = end(xts_irregular), 
                    by = "month")
print(regular_time)

## [1] "2022-01-01" "2022-02-01" "2022-03-01" "2022-04-01" "2022-05-01"
## [6] "2022-06-01" "2022-07-01"

Construct an Empty xts Object with Regular Frequency: Using the regularly spaced time index, initialize an empty xts object.
```
empty_xts <- xts(x = NULL, order.by = regular_time)
```

Merge the Irregular Data with the Empty xts Object: This step fills the gaps in your irregular dataset with NA values, corresponding to the dates in the regular xts object where data isn’t available.

xts_regular <- merge(xts_irregular, empty_xts)
print(xts_regular)

##            xts_irregular
## 2022-01-01             1
## 2022-02-01             2
## 2022-03-01            NA
## 2022-04-01            NA
## 2022-05-01             3
## 2022-06-01            NA
## 2022-07-01             4

Dealing with Missing Values: When needed, address NA values using methods like na.locf(), na.fill(), or na.approx(), as detailed in Chapter 4.8.5.

xts_regular <- na.approx(xts_regular)
print(xts_regular)

##            xts_irregular
## 2022-01-01      1.000000
## 2022-02-01      2.000000
## 2022-03-01      2.314607
## 2022-04-01      2.662921
## 2022-05-01      3.000000
## 2022-06-01      3.508197
## 2022-07-01      4.000000

By utilizing these transformations in xts, you can refine your time series data into a format that’s more amenable for subsequent analyses.

4.8.8 Apply Family

In R, the apply family of functions offers a mechanism to perform repeated operations across data structures without the necessity for explicit loops. This becomes especially beneficial for time series data in xts objects when the task is to aggregate across temporal intervals, such as converting quarterly GDP data to an annual frequency.

Apply by Columns and Rows

Since an xts object is a matrix with an attached time index, the apply functions highlighted in Chapter 4.3.9 for matrices also work with xts objects. Specifically, the apply() function allows for the application of a function across entire columns or rows of an xts object. Additionally, more efficient alternatives like rowSums(), colSums(), colMeans(), and rowMeans() are available, and the sweep() function proves useful for time series normalization to specific mean and variance values.

Apply by Groups

As elaborated in Chapter @ref(apply-family-data.frame), the split-apply-combine strategy segments the rows of a data frame into distinct groups, applies functions like averages or minimum values per group, and then combines the summarized groups to a single data object. When engaging with an xts object, remember that every row refers to a time period. Consequently, a collection of rows denotes a time interval. Thus, using the split-apply-combine strategy on an xts object, for instance, to calculate the monthly mean within a year, effectively aggregates the time series data from a more granular frequency (like monthly) to a coarser one (like annually).

Whilte the split-apply-combine strategy for data frames revolves around the sequence: split() + lapply() + do.call() + c(), aggregating time-series data with xts objects extends the sequence as follows: endpoints() + cut() + split() + lapply() + do.call() + rbind(). The goal is to break the time series into relevant intervals using endpoints() + cut() + split(), apply a desired function to each interval using lapply(), and then combine the results into a single xts object using do.call() + rbind(). Here’s how to aggregate the provided monthly time series to a yearly frequency by computing the mean by year:

# Sample monthly time series
dates <- seq(from = as.Date("2022-10-01"), length.out = 8, by = "1 month")
sample_xts <- xts(c(100 + 1:7, NA), order.by = dates)
print(sample_xts)

##            [,1]
## 2022-10-01  101
## 2022-11-01  102
## 2022-12-01  103
## 2023-01-01  104
## 2023-02-01  105
## 2023-03-01  106
## 2023-04-01  107
## 2023-05-01   NA

endpoints(): This function within the xts package determines where in the data set the splits should be made.
```
# Identify endpoints for each year
end_points <- endpoints(x = sample_xts, on = "years", k = 1)
print(end_points)
```
```
## [1] 0 3 8
```
Here’s a breakdown of the endpoints() function inputs:
- x: This is the xts object you want to find the endpoints for. In our example, it’s the sample_xts dataset.
- on: Specifies the time unit to identify as endpoints. Options can be “seconds”, “minutes”, “hours”, “days”, “weeks”, “months”, “quarters”, or “years”. For our purpose, we’ve used “years”.
- k: This sets the frequency for marking endpoints. A k value of 1 combined with on = "years" will set endpoints at the conclusion of each year. However, if k were 2, endpoints would be identified every two years.
In our sample, the endpoints 0, 3, 8 indicate that observations at positions 0, 3, 8 are the terminal points for their respective years.
cut(): After pinpointing the endpoints, we need to segment the time index of the xts object based on these intervals. The cut() function facilitates this segmentation:
```
# Segment the time index into intervals
cut_time <- cut(x = seq_along(sample_xts), 
                breaks = end_points,
                labels = index(sample_xts)[end_points])
print(cut_time)
```
```
## [1] 2022-12-01 2022-12-01 2022-12-01 2023-05-01 2023-05-01 2023-05-01 2023-05-01
## [8] 2023-05-01
## Levels: 2022-12-01 2023-05-01
```
The function inputs are elaborated below:
- x: This refers to the sequence of numbers representing the row positions of the xts object. In essence, seq_along(sample_xts) generates a sequence from 1 to the length of sample_xts, corresponding to each row of our time series data.
- breaks: This parameter determines where to segment the data. Here, we utilize the positions established by the endpoints() function to mark where each interval begins and ends.
- labels: This argument assigns a name or label to each interval. In our scenario, we’ve used the actual dates from our xts object to label the intervals, marking each segment with the corresponding endpoint date.

split(): With the intervals defined, the xts object can be segmented using split() function based on the categories established by cut().

# Split data into time intervals
split_data <- split(x = sample_xts, f = cut_time)
print(split_data)

## $`2022-12-01`
##               
## 2022-10-01 101
## 2022-11-01 102
## 2022-12-01 103
## 
## $`2023-05-01`
##               
## 2023-01-01 104
## 2023-02-01 105
## 2023-03-01 106
## 2023-04-01 107
## 2023-05-01  NA

lapply(): After segmentation, lapply() can be harnessed to apply a specific function, like calculating an average, across each segment.
```
# Apply a function to the data of each time interval
monthly_means_list <- lapply(X = split_data, FUN = mean, na.rm = TRUE)
print(monthly_means_list)
```
```
## $`2022-12-01`
## [1] 102
## 
## $`2023-05-01`
## [1] 105.5
```
Observe that in the lapply() function, extra arguments are passed directly to the function specified in the FUN parameter. In this context, the supplementary argument na.rm = TRUE serves as an input to the mean function, equivalent to designating FUN = function(x) mean(x, na.rm = TRUE).

do.call() + rbind(): After processing each interval, the subsequent step is to combine the results into a unified xts object. The combination of do.call() and rbind() offers an efficient method for this task.

# Merging aggregated data into a matrix
combined_means_matrix <- do.call(what = rbind, args = monthly_means_list)

# Transitioning matrix to an xts format
aggregated_xts <- as.xts(combined_means_matrix)

# Display the consolidated data
print(aggregated_xts)

##             [,1]
## 2022-12-01 102.0
## 2023-05-01 105.5

It’s worth noting that during our use of the cut() function, we labeled each segment with its respective endpoint, i.e., labels = index(sample_xts)[end_points]. As a consequence, the merged data is indexed by the concluding date of each year. To modify this, such as setting it to the initial day of the year, one can tweak the index as follows:

# Adjusting the time index to reflect the first day of each corresponding year
index(aggregated_xts) <- as.Date(format(index(aggregated_xts), "%Y-01-01"))
print(aggregated_xts)

##             [,1]
## 2022-01-01 102.0
## 2023-01-01 105.5

The split-apply-combine strategy isn’t limited to producing a singular value for each group. Instead, it can also return multiple values or even a series of values. For instance, consider the goal of obtaining the cumulative product for each month:

# Computing the cumulative product for each time interval
monthly_cumprod_list <- lapply(X = split_data, FUN = cumprod)
print(monthly_cumprod_list)

## $`2022-12-01`
##                   
## 2022-10-01     101
## 2022-11-01   10302
## 2022-12-01 1061106
## 
## $`2023-05-01`
##                     
## 2023-01-01       104
## 2023-02-01     10920
## 2023-03-01   1157520
## 2023-04-01 123854640
## 2023-05-01        NA

# Consolidating the results into an xts object
aggregated_xts <- as.xts(do.call(what = rbind, args = monthly_cumprod_list))

# Displaying the aggregated results
print(aggregated_xts)

##                 [,1]
## 2022-10-01       101
## 2022-11-01     10302
## 2022-12-01   1061106
## 2023-01-01       104
## 2023-02-01     10920
## 2023-03-01   1157520
## 2023-04-01 123854640
## 2023-05-01        NA

Here, rather than condensing each month’s data into a single summary statistic, we’ve expanded each month’s data into a series representing the cumulative product.

Finally, there are several xts functions that simplify the split-apply-combine approach:

period.apply(): This function streamlines the split-apply-combine strategy. By determining the intervals using the endpoints, you can apply a function across these specified segments.
```
# Use period.apply() for aggregation
period.apply(sample_xts, INDEX = end_points, FUN = mean, na.rm = TRUE)
```
```
##             [,1]
## 2022-12-01 102.0
## 2023-05-01 105.5
```
apply.*(): The series of functions - apply.daily(), apply.weekly(), apply.monthly(), apply.quarterly(), and apply.yearly() - enable aggregation or transformation of time series data grounded on precise time intervals. Essentially, they act as specialized versions of the period.apply() function, designed for specific time frames.
```
# Yearly aggregation example
apply.yearly(sample_xts, FUN = mean, na.rm = TRUE)
```
```
##             [,1]
## 2022-12-01 102.0
## 2023-05-01 105.5
```
While these apply.*() functions simplify the split-apply-combine strategy, for unconventional aggregation frequencies, like quadrennial aggregations focusing on leap year endpoints, one would revert to the more intricate sequence: endpoints() + cut() + split() + lapply() + do.call() + rbind().

to.period(): Within financial time series data, the OHLC format is prevalent. It represents the Open, High, Low, and Close prices for assets within specific intervals, like daily, monthly, or yearly. The Open is the starting price, the High and Low represent the maximum and minimum prices achieved, respectively, and the Close is the ending price. This quartet offers insights into price movements and volatility within the given time span.

# OHLC aggregation with to.period()
to.period(sample_xts, period = "years")

##            sample_xts.Open sample_xts.High sample_xts.Low sample_xts.Close
## 2022-12-01             101             103            101              103
## 2023-04-01             104             107            104              107

# OHLC aggregation without to.period()
OHLC_functions <- list(Open = function(x) head(na.omit(x), 1), 
                       High = function(x) max(x, na.rm = TRUE), 
                       Low = function(x) min(x, na.rm = TRUE), 
                       Close = function(x) tail(na.omit(x), 1))
sapply(X = OHLC_functions, FUN = apply.yearly, x = sample_xts)

##      Open High Low Close
## [1,]  101  103 101   103
## [2,]  104  107 104   107

Apply by Overlapping Groups

In time series analysis, there are occasions when you need to apply a function to overlapping periods or windows of data rather than distinct, non-overlapping intervals. This distinction brings into focus two types of time windows, illustrated in Figure 4.2:

Figure 4.2: Time Windows

Tumbling Window: Also known as a fixed window, this method uses a stable start or endpoint for the window and aggregates data based on that anchor. A common illustration is when transitioning from monthly data to yearly data, where each year represents a separate, non-overlapping group of 12 months.
Sliding Window: Alternatively called a rolling window, this method allows the window to “slide” over time. Both the beginning and the end of the window shift with each step, consistently encompassing a fixed number of periods. This approach produces a continuous sequence of averages (or other aggregates) and is particularly beneficial for observing smooth temporal trends. For instance, if you apply a 12-month sliding window to monthly data, it would calculate a moving average for every subsequent 12-month segment.

In financial time series contexts, metrics such as rolling volatility or moving averages often necessitate the examination of sliding windows instead of tumbling windows. The rollapply() function in the xts package provides an efficient solution for these scenarios.

Let’s dive deeper into the rollapply() function using an example.

Consider a financial market dataset eq_mkt that contains daily returns, and you’re interested in computing the rolling standard deviation (volatility) for a 3-day window. Instead of using non-overlapping 3-day chunks, you want every single 3-day interval. This means the first calculation would be for days 1-3, the second for days 2-4, the third for days 3-5, and so on.

# Sample dataset creation
dates <- seq(from = as.Date("2022-01-01"), length.out = 10, by = "1 day")
eq_mkt <- xts(rnorm(10, 0, 0.02), order.by = dates)
print(eq_mkt)

##                     [,1]
## 2022-01-01  0.0003441055
## 2022-01-02  0.0324251170
## 2022-01-03 -0.0097666865
## 2022-01-04 -0.0106594578
## 2022-01-05 -0.0565918501
## 2022-01-06 -0.0010790750
## 2022-01-07  0.0092368230
## 2022-01-08  0.0265243524
## 2022-01-09 -0.0179893312
## 2022-01-10  0.0504600364

# Application of rollapply()
rolling_volatility <- rollapply(eq_mkt, width = 3, FUN = sd)
print(rolling_volatility)

##                  [,1]
## 2022-01-01         NA
## 2022-01-02         NA
## 2022-01-03 0.02202865
## 2022-01-04 0.02462122
## 2022-01-05 0.02678052
## 2022-01-06 0.02967388
## 2022-01-07 0.03540598
## 2022-01-08 0.01394767
## 2022-01-09 0.02244100
## 2022-01-10 0.03473639

Here’s a breakdown of the rollapply() function and its parameters:

data: This is the xts object (or any time-series object) on which you want to apply the function. In our example, it’s the eq_mkt dataset.
width: Specifies the size of the rolling window. Here, we’ve chosen a width of 3, which means we’ll compute the standard deviation for every 3-day overlapping period.
FUN: The function you want to apply to each rolling window. We’ve used sd to compute the standard deviation, but it could be any other function, such as mean for a moving average.

The output is an xts object containing the result of the function applied to each rolling window. Note that the resulting time series will be shorter than the original by width - 1, since the first width - 1 observations don’t have enough data points before them to form a complete window.

This approach is extremely versatile and powerful. By changing the width parameter and the function applied (FUN), you can compute a variety of rolling statistics. The concept of overlapping periods is crucial in financial analysis, particularly for calculating metrics that provide insights into short-term dynamics and potential trend changes.

4.8.9 Resources

To delve deeper into xts and zoo objects, consider reading its vignette, by executing vignette("xts", package = "xts"), as well as exploring the following DataCamp courses:

If you’re working within the tidyverse environment, the R package tidyquant by Dancho and Vaughan (2023) offers seamless integration with xts and zoo, see vignette("TQ02-quant-integrations-in-tidyquant", package = "tidyquant"). Lastly, the following handy cheat sheet provides a quick reference on xts and zoo functions: s3.amazonaws.com/assets.datacamp.com/blog_assets/xts_Cheat_Sheet_R.pdf.

References

Barrett, Tyson, Matt Dowle, Arun Srinivasan, Jan Gorecki, Michael Chirico, and Toby Hocking. 2024. Data.table: Extension of ‘Data.frame‘. https://r-datatable.com. R package version 1.15.2.

Bates, Douglas, Martin Maechler, and Mikael Jagan. 2024. Matrix: Sparse and Dense Matrix Classes and Methods. https://Matrix.R-forge.R-project.org. R package version 1.6-5.

Dancho, Matt, and Davis Vaughan. 2023. Tidyquant: Tidy Quantitative Financial Analysis. https://github.com/business-science/tidyquant. R package version 1.0.7.

Maechler, Martin, Christophe Dutang, and Vincent Goulet. 2024. Expm: Matrix Exponential, Log, Etc. https://R-Forge.R-project.org/projects/expm/. R package version 0.999-9.

Müller, Kirill, and Hadley Wickham. 2023. Tibble: Simple Data Frames. https://tibble.tidyverse.org/. R package version 3.2.1.

———. 2024b. Xts: eXtensible Time Series. https://joshuaulrich.github.io/xts/. R package version 0.13.2.

———. 2023c. Tidyverse: Easily Install and Load the Tidyverse. https://tidyverse.tidyverse.org. R package version 2.0.0.

Wickham, Hadley, Romain François, Lionel Henry, Kirill Müller, and Davis Vaughan. 2023. Dplyr: A Grammar of Data Manipulation. https://dplyr.tidyverse.org. R package version 1.1.4.

Wickham, Hadley, and Lionel Henry. 2023. Purrr: Functional Programming Tools. https://purrr.tidyverse.org/. R package version 1.0.2.

Wickham, Hadley, Davis Vaughan, and Maximilian Girlich. 2024. Tidyr: Tidy Messy Data. https://tidyr.tidyverse.org. R package version 1.3.1.

Zeileis, Achim, Gabor Grothendieck, and Jeffrey A. Ryan. 2023. Zoo: S3 Infrastructure for Regular and Irregular Time Series (z’s Ordered Observations). https://zoo.R-Forge.R-project.org/. R package version 1.8-12.

Chapter 4 Data Structures in R

4.1 Scalar

4.2 Vector

4.3 Matrix (matrix)

4.3.1 Create a Matrix

4.3.2 Inspect a Matrix

4.3.3 Select and Modify

4.3.4 Add Labels

4.3.5 Handle Missing Values

4.3.6 Element-Wise Operations

4.3.7 Linear Algebra Operations

4.3.8 Combine Matrices

4.3.9 Apply Family

4.4 List (list)

4.4.1 Create a List

4.4.2 Inspect a List

4.4.3 Select and Modify

4.4.4 Add Labels

4.4.5 Combine Lists

4.4.6 Apply Family

4.5 Data Frame (data.frame)

4.5.1 Create a Data Frame

4.5.2 Inspect a Data Frame

4.5.3 Select and Modify

The with() Function

4.5.4 Add Labels

4.5.5 Handle Missing Values

4.5.6 Combine Data Frames

4.5.7 Apply Family

Apply by Columns and Rows

Apply by Groups

4.5.8 Reshape Data Frames

4.6 Tibble (tbl_df)

4.6.1 Create a Tibble

4.6.2 Inspect a Tibble

4.6.3 Select and Modify

Select and Order Columns

Filter and Order Rows

Add and Remove Columns

Manipulate Columns

Use the Pipe Operator

4.6.4 Add Labels

4.6.5 Handle Missing Values

4.6.6 Combine Tibbles

4.6.7 Apply Family

Apply by Columns and Rows

Apply by Groups

4.6.8 Reshape Tibbles

4.7 Data Table (data.table)

4.8 Extensible Time Series (xts)

4.8.1 Create an xts Object

4.8.2 Inspect an xts Object

4.8.3 Select and Modify

4.8.4 Add Labels

4.8.5 Handle Missing Values

4.8.6 Combine xts Objects

Align Time Indices

4.8.7 Time Series Transformations

Lag Time Series

Convert Levels to Changes

Make Time Series Regular

4.8.8 Apply Family

Apply by Columns and Rows

Apply by Groups

Apply by Overlapping Groups

4.8.9 Resources

References

4.3 Matrix (`matrix`)

4.4 List (`list`)

4.5 Data Frame (`data.frame`)

The `with()` Function

4.6 Tibble (`tbl_df`)

4.7 Data Table (`data.table`)

4.8 Extensible Time Series (`xts`)

4.8.1 Create an `xts` Object

4.8.2 Inspect an `xts` Object